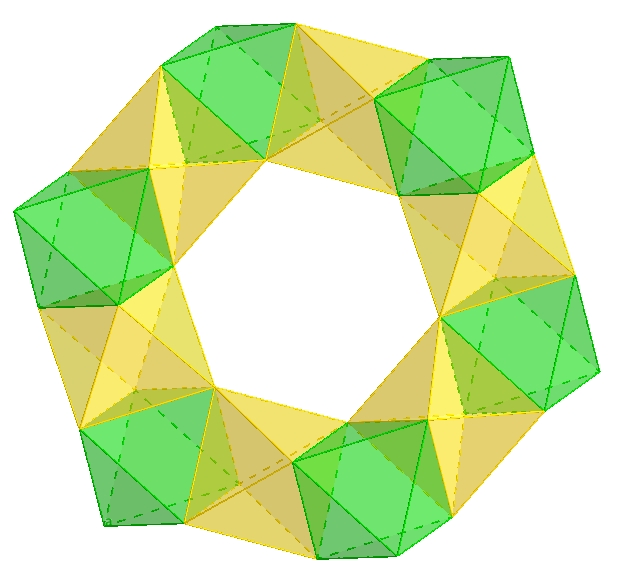
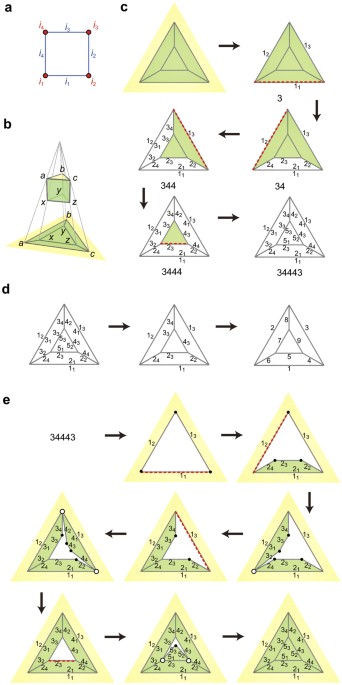
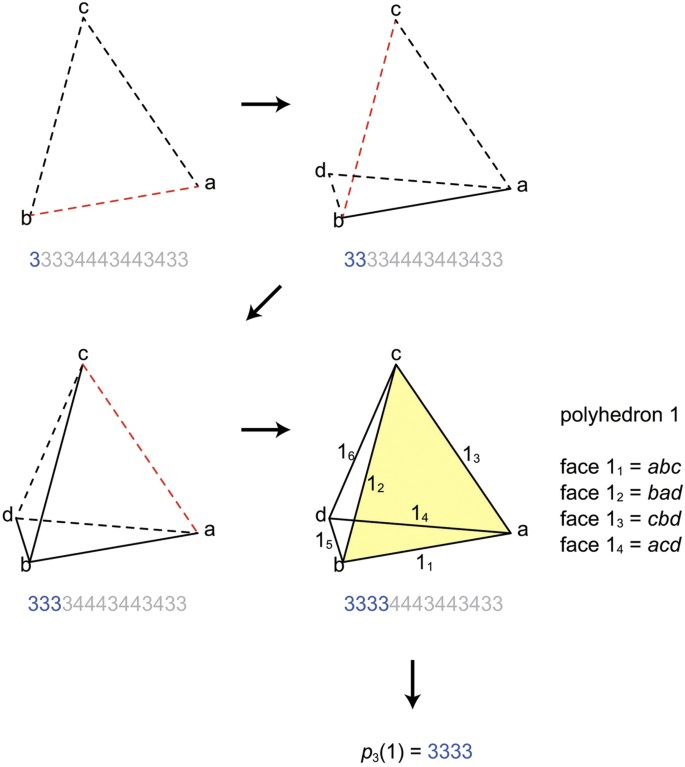
Topology is a branch of mathematics that examines the properties of geometric objects that are preserved through deformations such as stretching, bending, and twisting. One fascinating aspect of topology is the study of polyhedra, which are three-dimensional shapes consisting of flat polygonal faces, straight edges, and sharp vertices. While polyhedra are commonly encountered in everyday life, their intricate structures and properties hold great significance in various fields.
Galxe polyhedra are an intriguing class of polyhedra that have captured the attention of topologists. These exceptional structures possess unique properties that make them invaluable in the field of topology. Galxe polyhedra are characterized by their irregular configurations, non-convex faces, and exotic symmetries. These features set them apart from traditional polyhedra and make them a subject of intense exploration for topological researchers.
One of the key reasons for the importance of galxe polyhedra lies in their ability to provide insight into the fundamental principles of topology. Their intricate arrangements allow mathematicians to study the behavior of surfaces and spaces in a controlled and systematic manner. The study of galxe polyhedra helps unveil the underlying concepts of connectivity, dimensionality, and transformation, shedding light on the complex interplay between geometry and topology.
Galxe polyhedra play a crucial role in the field of topology, a branch of mathematics that studies the properties of space that are preserved under continuous transformations. These polyhedra, which are three-dimensional geometric shapes composed of straight-edged polygons, have proven to be valuable tools for understanding the fundamental concepts of topology.
One of the main reasons why galxe polyhedra are significant in topology is their ability to represent the connectivity of spaces. These polyhedra can be used to model and study the relationships between different regions of space, enabling mathematicians to analyze complex topological structures in a more tangible and understandable way.
Galxe, a popular software application developed specifically for working with galxe polyhedra, has greatly contributed to the importance of these shapes in topology. With its user-friendly interface and powerful features, Galxe has attracted a large community of mathematicians and researchers who rely on it for their topological studies.
In conclusion, galxe polyhedra provide a visually intuitive and practical approach to studying topology. Their ability to represent the connectivity of spaces, combined with the convenience of software applications like Galxe, has made them indispensable tools for mathematicians and researchers in the field.
Galxe polyhedra are a fascinating class of geometric objects that have found numerous applications in the field of topology. These multi-dimensional structures have garnered significant attention from researchers due to their unique properties and their ability to represent complex topological relationships.
One of the main applications of galxe polyhedra is in the study of manifolds. A manifold is a topological space that locally resembles Euclidean space. Galxe polyhedra provide a useful framework for understanding the connectivity and structure of manifolds. Their intricate network of edges and vertices allows researchers to analyze the relationships between different regions of a manifold and study its behavior in a systematic manner.
Knot theory is another area where galxe polyhedra have proven to be invaluable. Knot theory is the study of mathematical knots, which are closed curves embedded in three-dimensional space. Galxe polyhedra can be used to represent complex knots and analyze their properties. By representing knots as galxe polyhedra, researchers gain insight into the topology of the knot and can explore its various characteristics, such as its genus, symmetry, and chirality.
In the field of geometric topology, galxe polyhedra have also made significant contributions. Geometric topology is concerned with the properties of spaces that are preserved under continuous transformations, such as stretching or bending. Galxe polyhedra serve as a powerful tool for representing and studying these spaces, allowing researchers to investigate their properties and discover new theorems and conjectures.
Furthermore, galxe polyhedra find applications in graph theory. Graph theory is the study of mathematical structures used to model pairwise relationships between objects. Galxe polyhedra can be used to represent graphs, and their connectivity properties can be analyzed to gain insights into the underlying relationships within the graph. This application has proven to be particularly useful in fields such as computer science and network analysis.
In conclusion, the applications of galxe polyhedra in topology are diverse and far-reaching. They provide a unique perspective on the topological properties of manifolds, knots, spaces, and graphs. The use of galxe polyhedra in these areas has resulted in significant advancements and deepened our understanding of the intricate relationships present in the field of topology.
Galxe polyhedra are fascinating geometric structures that have gained a lot of attention in the field of topology. These three-dimensional solids are composed of regular polygons that intersect to form a closed surface.
One of the key aspects of galxe polyhedra is their unique structure. Unlike traditional polyhedra such as cubes or tetrahedra, galxe polyhedra have irregular faces that intersect at different angles. This creates a complex, yet visually striking, arrangement of polygons.
Galxe polyhedra have been extensively studied in the field of topology due to their interesting topological properties. They are known for having a high degree of symmetry and exhibiting different levels of connectivity between their faces and vertices.
Vertex-Transitivity: Galxe polyhedra are vertex-transitive, meaning that each vertex can be transformed into any other vertex by a symmetry operation. This property contributes to their overall aesthetically pleasing appearance.
Edge-Transitivity: Similarly, galxe polyhedra are also edge-transitive, which means that each edge can be transformed into any other edge through a symmetry operation.
Spherical Symmetry: Many galxe polyhedra exhibit spherical symmetry, meaning that their faces are arranged in such a way that the polyhedra can fit perfectly inside a sphere.
These topological properties make galxe polyhedra an interesting subject of study for mathematicians and scientists alike. They provide insights into the underlying structure and symmetry of three-dimensional solids and offer countless possibilities for further exploration and research.
Network analysis is a vital tool in our modern interconnected world. From social networks to computer networks, understanding the structure and dynamics of these systems is crucial for detecting patterns, identifying vulnerabilities, and optimizing efficiency.
One key concept in network analysis is the use of mathematical models to represent and analyze the underlying structure of a network. One such model that has gained significant attention recently is the galxe polyhedra.
Galxe polyhedra are a class of geometric polyhedra that can be used to represent the complex connectivity of networks. These polyhedra are characterized by their unique properties, including their ability to capture both local and global network features.
Unlike traditional network models, which often simplify the structure of a network by focusing only on node connections or edge relationships, galxe polyhedra offer a more holistic representation of the network. They capture not only the direct connections between nodes but also the higher-order relationships and clustering properties.
The use of galxe polyhedra in network analysis provides several advantages. Firstly, they enable a more accurate representation of the network structure, allowing for a deeper understanding of the system's dynamics and behavior.
Secondly, galxe polyhedra allow for the identification of specific network patterns and motifs that may be critical for the network's functionality. By analyzing the geometric properties of the polyhedra, network analysts can detect recurring patterns that may indicate key nodes, central hubs, or bottlenecks within the network.
Additionally, galxe polyhedra offer a powerful visualization tool for network analysis. By representing the network as a three-dimensional polyhedron, it becomes easier to comprehend and explore the complex connectivity and relationships within the network.
Overall, the inclusion of galxe polyhedra in network analysis opens up new avenues for studying and understanding complex networks. Their unique properties and representations provide valuable insights into the structure, dynamics, and behavior of various types of networks, from social networks to biological networks and beyond.
In conclusion, galxe polyhedra play a significant role in network analysis by offering a more comprehensive representation of the underlying network structure and providing insights into key network patterns and motifs. They are a valuable mathematical tool that enables researchers and analysts to study and optimize various types of networks in our interconnected world.
In the field of 3D modeling and simulation, galxe polyhedra have emerged as a powerful tool with numerous applications. These unique structures, also known as Goldberg-Coxeter transformations, play a vital role in creating complex geometric shapes and modeling real-world objects with precision and accuracy.
One of the key advantages of galxe polyhedra is their ability to tessellate space. With their intricate and symmetrical patterns, they can be used to generate highly detailed meshes that accurately represent physical objects or environments. This property makes them invaluable in various industries, including architecture, engineering, and computer graphics.
Furthermore, galxe polyhedra provide a solid foundation for simulating and analyzing intricate systems. Whether it's simulating fluid dynamics, modeling molecular structures, or studying the behavior of complex networks, these polyhedra offer a versatile framework for understanding and visualizing complex systems in three dimensions.
The application of galxe polyhedra extends beyond static models and simulations. They can also be utilized in the field of virtual reality and game development, providing visually stunning and realistic environments for immersive experiences. By leveraging the power of galxe polyhedra, designers and developers can create captivating virtual worlds that simulate real-world physics and interactions.
In addition to their practical applications, galxe polyhedra also have significant theoretical implications in the field of topology. They offer a rich source of study for mathematicians, allowing for the exploration of various geometric transformations and the understanding of spatial relationships between objects.
In conclusion, galxe polyhedra play a crucial role in 3D modeling and simulation. Their ability to tessellate space, simulate complex systems, and create visually appealing environments make them an invaluable tool in various industries. Furthermore, their theoretical significance in topology further solidifies their importance in the field. As technology advances, galxe polyhedra will continue to shape the way we model, simulate, and understand our world in three dimensions.
The study of galxe polyhedra involves the exploration of their intricate symmetry patterns, which play a crucial role in the field of topology. By understanding the symmetries of galxe polyhedra, researchers are able to gain insights into the underlying structures and properties of these fascinating geometric objects.
One of the most important aspects of analyzing the symmetry of galxe polyhedra is the identification of their symmetry groups. The symmetry group of a galxe polyhedron consists of all the transformations or motions that preserve its shape and structure. These transformations can include rotations, reflections, and translations.
To analyze the symmetry of a galxe polyhedron, mathematicians often use symmetry notation such as Schönflies notation or Hermann-Mauguin notation. These notations allow researchers to describe and categorize the different types of symmetry exhibited by galxe polyhedra.
Another important concept in analyzing the symmetry of galxe polyhedra is the notion of symmetry breaking. Symmetry breaking occurs when the symmetry of a galxe polyhedron is reduced due to external factors or constraints. This phenomenon is of particular interest in topology, as it can lead to the emergence of new and unexpected properties in the polyhedral structure.
Furthermore, the symmetry of galxe polyhedra can be analyzed using various mathematical techniques, such as group theory and crystallography. These techniques provide a rigorous framework for understanding the symmetries and transformations of galxe polyhedra, allowing researchers to make precise and systematic investigations into their properties.
Overall, analyzing the symmetry of galxe polyhedra is a fundamental aspect of studying these geometric objects in the field of topology. By understanding their symmetries, researchers can gain valuable insights into their structures and properties, paving the way for further advancements in the field.
In the field of mathematics, galxe polyhedra and graph theory are closely interconnected. Galxe polyhedra, which are also known as space-filling polyhedra, play a significant role in the study of topology and have direct applications in graph theory.
Galxe polyhedra are three-dimensional geometric structures consisting of congruent polygons that fill space without leaving any gaps. They are a special type of polyhedron that can be used to divide three-dimensional space into smaller, discrete regions. These polyhedra have been extensively studied in the field of topology due to their unique properties and applications.
Graph theory is a branch of mathematics that deals with the study of graphs, which are mathematical representations of networks or connections between objects. Galxe polyhedra have a direct connection to graph theory as they can be used to construct graphs with specific properties.
By considering the edges and vertices of a galxe polyhedron, a graph can be formed where each vertex represents a polygon and each edge represents a shared side between two polygons. This graph can capture the connectivity and relationships between the polygons in the polyhedron, and can be used to analyze the structure and properties of the galxe polyhedron.
Furthermore, graph theory provides a mathematical framework to study the connectivity and graph properties of galxe polyhedra. Concepts such as Eulerian cycles, planarity, and graph coloring can be applied to galxe polyhedra graphs, yielding important insights into their structure and topological properties.
Galxe polyhedra have been widely used in the field of topology to study and classify different types of polyhedra. They serve as important building blocks in the construction of more complex polyhedra and can provide a deeper understanding of the topological properties of these structures.
Furthermore, the study of galxe polyhedra has led to the development of algorithms and computational methods for generating and analyzing polyhedral structures. These methods have direct applications in various fields, including architecture, materials science, and computer graphics.
Galxe polyhedra have been used in architectural design to create unique and aesthetically pleasing structures by utilizing their space-filling properties.
In materials science, galxe polyhedra are investigated for their potential applications in the creation of new materials with desirable properties.
In computer graphics, galxe polyhedra are utilized to generate realistic 3D models and simulate complex physical phenomena.
In conclusion, the relationship between galxe polyhedra and graph theory is fundamental to the study of topology. Galxe polyhedra provide a concrete geometric representation that can be analyzed using graph theory concepts, yielding important insights into their structure and properties. Furthermore, the study of galxe polyhedra has practical applications in various fields, making them a topic of ongoing research and exploration.
Galxe polyhedra, also known as polyhedral surfaces, play a crucial role in the field of topology. These three-dimensional objects are composed of polygonal faces that meet at vertices and are connected by edges. In topology, galxe polyhedra are used to understand and analyze the properties and characteristics of various surfaces.
A galxe polyhedron is defined as a collection of faces, edges, and vertices that satisfies certain conditions. The faces are planar and can be of any shape, such as triangles, squares, or pentagons. The edges are straight and connect the vertices, while the vertices are points where the edges meet. Galxe polyhedra can be represented mathematically using graphs, networks, or matrices.
Galxe polyhedra are extensively used in the study of surfaces. They help researchers classify surfaces based on their topological properties, such as their genus, connectivity, and orientability. By analyzing the arrangement and connectivity of faces, edges, and vertices in galxe polyhedra, researchers can gain insights into the properties of surfaces.
One important concept related to galxe polyhedra is the Euler characteristic, which is a numerical invariant of a surface. It represents the number of faces minus the number of edges plus the number of vertices. This characteristic can be used to determine the genus of a surface, which is a measure of its complexity.
Sphere
2
0
Torus
0
1
Double Torus
-2
2
In addition to classifying surfaces, galxe polyhedra also aid in the visualization and representation of complex surfaces. By constructing galxe polyhedra that approximate the shape of a given surface, researchers can study and analyze its properties more easily.
In conclusion, galxe polyhedra are an essential tool in the field of topology for understanding and studying surfaces. They provide a visual and mathematical framework to analyze the properties of surfaces, classify them based on their topological characteristics, and aid in the representation of complex surfaces.
Galxe polyhedra have garnered significant attention in the field of topology due to their unique and intriguing properties. These intricate geometric structures, consisting of a combination of hexagons and pentagons, are known for their ability to form fullerenes and nanotubes, which have found applications in various scientific and technological fields.
Researchers have focused on investigating the topological properties of galxe polyhedra to better understand their structure and potential applications. By examining their connectivity, surface area, and other geometric characteristics, scientists can unravel the underlying principles that govern these complex structures.
One of the key properties studied is the Euler characteristic, which is a topological invariant. It relates the number of vertices, edges, and faces of a galxe polyhedron. Through rigorous mathematical analysis, researchers have identified interesting relationships between the Euler characteristic and the connectivity of these polyhedra, shedding light on the way these structures are constructed and their stability.
The analytical understanding of the topological properties of galxe polyhedra has paved the way for their applications in materials science and nanotechnology. The ability to manipulate the connectivity of these structures allows scientists to control important physical and chemical properties, such as thermal conductivity and mechanical strength.
Furthermore, galxe polyhedra have shown potential in the design of advanced materials with tailored properties. By combining galxe polyhedra with other nanostructures, scientists can create innovative materials with enhanced functionalities, such as improved catalytic activity or tunable optical properties.
Galxe polyhedra-based materials have shown promise in various fields, including energy storage, drug delivery systems, and catalysis.
The unique topology of galxe polyhedra provides a robust framework for the design of self-assembled nanoarchitectures, leading to the creation of novel nanomaterials.
By exploring their topological properties, researchers can further optimize the structural and functional properties of galxe polyhedra, opening up new possibilities in nanotechnology and materials science.
In conclusion, the investigation of the topological properties of galxe polyhedra is crucial for both theoretical understanding and practical applications. The knowledge gained from these investigations enables the design of novel materials with tailored properties, advancing the fields of materials science and nanotechnology.
What are galxe polyhedra?
Galxe polyhedra are a type of geometric shape that have special properties in the field of topology. They are constructed using a specific algorithm that allows for their unique properties and shape.
How are galxe polyhedra used in topology?
Galxe polyhedra play a crucial role in the field of topology. They can be used to study the properties of various mathematical structures and help in understanding complex spaces and their dimensions.
What are the applications of galxe polyhedra in real life?
The applications of galxe polyhedra in real life are diverse. They have applications in computer graphics, architecture, physics, and engineering. For example, in computer graphics, galxe polyhedra can be used to create visually appealing 3D models.
How are galxe polyhedra different from regular polyhedra?
Galxe polyhedra differ from regular polyhedra in terms of their shape and properties. While regular polyhedra have a specific set of regular faces and vertices, galxe polyhedra have irregular faces and vertices, which gives them unique topological properties.
Can galxe polyhedra have an infinite number of faces?
Yes, galxe polyhedra can have an infinite number of faces. This is one of their defining characteristics and allows for their study in infinite-dimensional spaces, which is important in certain areas of mathematics and physics.
What is the significance of galxe polyhedra in topology?
Galxe polyhedra play a crucial role in topology as they provide a geometric representation of certain abstract mathematical concepts. They allow mathematicians to study and analyze the properties and relationships of shapes and figures in a tangible and visual way.
How are galxe polyhedra different from regular polyhedra?
Galxe polyhedra differ from regular polyhedra in that they have a more complex structure and can have irregular faces and edges. While regular polyhedra have symmetrical and identical faces, galxe polyhedra can have uneven faces and edges, allowing for more flexibility in their topology.
What are some practical applications of galxe polyhedra in the real world?
The practical applications of galxe polyhedra in the real world are vast and varied. They are used in computer graphics and animation to create realistic 3D models, in architecture and design to understand and optimize structural integrity, and in physics to study the properties of matter and explore the behavior of particles.
Are there any limitations to using galxe polyhedra in topology?
While galxe polyhedra are a valuable tool in topology, they do have some limitations. Due to their complex structure, analyzing and calculating properties of galxe polyhedra can be challenging and time-consuming. Additionally, their irregular shapes may not always accurately represent certain abstract mathematical concepts.
Can galxe polyhedra be used to study higher dimensions beyond three-dimensional space?
Yes, galxe polyhedra can indeed be used to study higher dimensions beyond three-dimensional space. In topology, mathematicians often work with abstract geometric objects that exist in higher dimensions, and galxe polyhedra provide a way to visualize and understand these higher-dimensional structures in a more concrete and intuitive manner.
2022-2024 @ Exploring the importance of galxe polyhedra in the field of topology
Curious about the popularity of Galxe? Find out on their website!