Galxe login | Galxe ID | Passport | Explore Campaigns | Galxe products
Galxe login | Galxe ID | Passport | Explore Campaigns | Galxe products
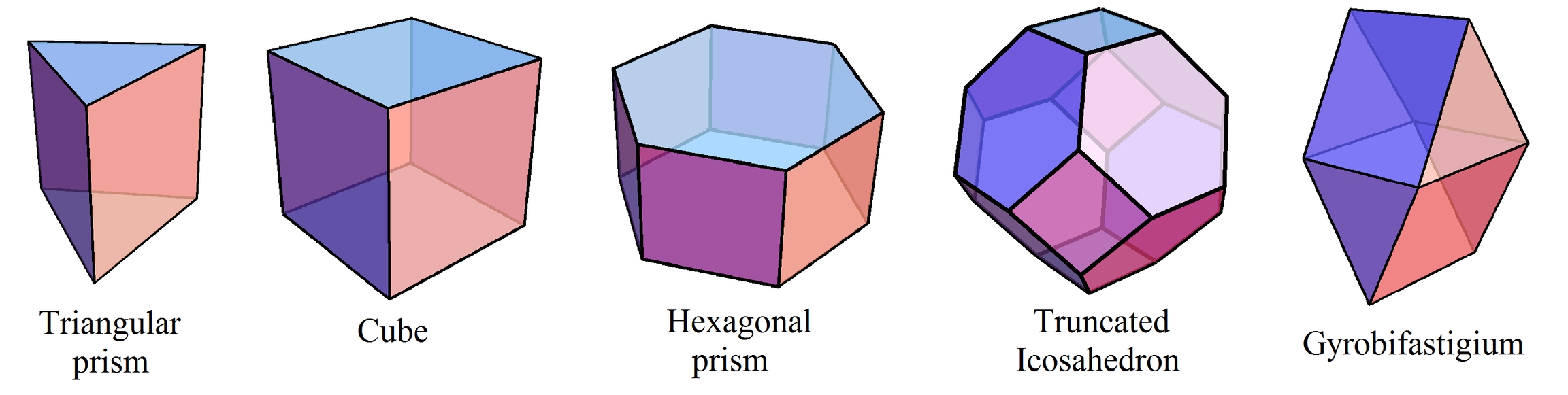
In the vast expanse of the universe, our fascination with the mysteries of space knows no bounds. From the twinkling stars to the swirling galaxies, the cosmos has captivated our imaginations for centuries. One such captivating aspect of space is the formation of polyhedra, three-dimensional shapes that fill space in a unique way.
The study of space-filling polyhedra is an intriguing branch of mathematics that delves into the intricate patterns and symmetries found in the universe. These polyhedra, also known as honeycombs, are formed by repeating a specific geometric shape to fill space without any gaps or overlaps. They can be found in diverse structures, from the microscopic world of crystals to the grandeur of galactic formations.
Exploring these mathematical properties can unlock a deeper understanding of the fundamental laws that govern the cosmos. By studying the symmetries and patterns of space-filling polyhedra, mathematicians can uncover the secrets of how matter organizes itself on both microscopic and macroscopic scales. This knowledge has practical applications in fields such as architecture, chemistry, and physics.
Furthermore, space-filling polyhedra have captivated artists and architects throughout history. The intricate designs and symmetries found in these structures have inspired works of art, from intricate mosaics to modern structural designs. By understanding the mathematical properties of space-filling polyhedra, artists and architects can create visually stunning works that mimic the beauty and harmony found in the universe.
In this article, we will delve into the fascinating world of space-filling polyhedra. We will explore their mathematical properties, their applications in various fields, and the artistic inspiration they provide. Join us on this journey through the intricate patterns and symmetries of the cosmos as we unravel the secrets of space-filling galactic polyhedra.
In the field of mathematics, exploring the mathematical properties of space filling galaxy polyhedra is an intriguing and complex task. These fascinating shapes have captivated mathematicians for centuries, as they offer a unique combination of aesthetic beauty and mathematical complexity.
One way to gain a better understanding of these polyhedra is through the study of their mathematical properties. By delving into their geometric features, symmetries, and mathematical relationships, mathematicians can uncover hidden patterns and structures that contribute to their beauty and functionality.
Galxe - Project Overview, Analytics, and Data
The exploration of mathematical properties involves conducting rigorous analysis and calculations to unveil the intricacies of these polyhedra. Mathematicians employ various mathematical techniques, such as topology, group theory, and differential geometry, to investigate the properties of space filling galaxy polyhedra.
These mathematical properties not only shed light on the structure of these polyhedra but also have practical applications in fields like architecture, design, and computer science. By understanding the mathematical properties of these shapes, we can create more efficient and visually appealing structures, develop algorithms for computer graphics and simulations, and gain insights into the fundamental principles of symmetry and geometry.
The study of mathematical properties is a collaborative effort involving mathematicians, computer scientists, and researchers from various disciplines. By leveraging advanced computational tools, data analysis techniques, and visualization technologies, researchers can explore and analyze large datasets of space filling galaxy polyhedra to uncover new mathematical properties.
Overall, the exploration of the mathematical properties of space filling galaxy polyhedra is an exciting and challenging endeavor. It not only contributes to our understanding of fundamental mathematical concepts but also inspires new discoveries and innovations in various fields. Galxe - Project Overview, Analytics, and Data provides a comprehensive platform for researchers to share their findings, collaborate on projects, and advance the study of mathematical properties.
Space filling galaxy polyhedra are fascinating mathematical objects that have been extensively studied in the field of geometry. These polyhedra are constructed by taking a regular polyhedron and repeatedly dividing each face into smaller polygons, which are then attached together to form a three-dimensional structure. The resulting polyhedra fill space without leaving any gaps, hence the name "space filling".
One of the most well-known examples of a space filling galaxy polyhedron is the Menger sponge. The Menger sponge is made by taking a cube and dividing each face into nine smaller squares, and then repeating this process recursively. The resulting structure is a fractal object that has an infinite number of layers, and fills space completely.
Space filling galaxy polyhedra have several interesting properties. Firstly, they have a high degree of symmetry, which means that they can be rotated or reflected in multiple ways without changing their appearance. This symmetry is often associated with aesthetically pleasing and visually striking patterns.
Secondly, space filling galaxy polyhedra have a fractal nature. Fractals are geometric shapes that exhibit self-similarity at different scales. This means that at different levels of magnification, the structure of the polyhedron looks similar to its overall shape. Fractals are found in many natural phenomena, such as clouds, coastlines, and tree branches.
The study of space filling galaxy polyhedra is a complex and interdisciplinary field that combines techniques from mathematics, computer science, and physics. Researchers in this field are interested in understanding the underlying mathematical principles that govern the behavior of these polyhedra, as well as their potential applications in various domains.
One area of research is focused on exploring the different types of space filling galaxy polyhedra that can be constructed. Researchers have discovered many different types of polyhedra, each with its own unique properties and characteristics. These discoveries have opened up new avenues for understanding the geometrical structure of space and the nature of three-dimensional space filling.
Another area of research is concerned with the computational aspects of space filling galaxy polyhedra. Researchers are developing algorithms and techniques for efficiently generating and manipulating these polyhedra, as well as for visualizing and analyzing their complex structures.
In conclusion, space filling galaxy polyhedra are fascinating mathematical objects that have captured the imaginations of researchers and enthusiasts alike. They possess unique properties and exhibit intricate geometrical structures. The study of these polyhedra not only deepens our understanding of the mathematical properties of space, but also has potential applications in various scientific and technological fields.
Galaxie polyhedra are geometric structures that fill three-dimensional space in a highly symmetric pattern. They are formed by interlocking identical polygons, known as tiles, in a way that maximizes their symmetry. The beauty of galaxie polyhedra lies in their intricate and captivating geometry.
One of the key aspects of galaxie polyhedra is their dimensionality. These structures are three-dimensional, meaning they occupy three axes of space: length, width, and height. This gives them a sense of depth and volume, making them visually striking and aesthetically pleasing.
Galaxie polyhedra exhibit a variety of geometrical properties. Firstly, they possess rotational symmetry, which means they can be rotated by certain angles and still retain their original appearance. This rotational symmetry is often associated with the presence of a central axis of rotation.
Furthermore, galaxie polyhedra can have reflectional symmetry, where they can be reflected across a plane and appear unchanged. This reflectional symmetry adds to their overall visual appeal and elegance.
Another interesting property of galaxie polyhedra is their vertex configuration. The vertices, or points where the polygons meet, are arranged in a specific way that ensures the polyhedra's overall symmetry. These vertex configurations can vary depending on the specific type of galaxie polyhedra.
Lastly, the faces of galaxie polyhedra are composed of identical polygons. These faces are arranged in a regular pattern, creating a consistent and harmonious visual effect. The combination of regular faces, symmetric vertex configurations, and three-dimensional structure gives galaxie polyhedra their unique charm.
In conclusion, galaxie polyhedra exhibit fascinating geometrical properties that make them a subject of both mathematical study and artistic admiration. Their three-dimensional nature, rotational and reflectional symmetry, vertex configurations, and regular face patterns contribute to their overall beauty and appeal. Exploring the dimensions and geometry of galaxie polyhedra opens up new avenues of mathematical and geometrical research.
Polyhedral space filling, also known as space-filling polyhedra, and mathematical puzzles are two fascinating areas of study that intertwine in unexpected and intriguing ways. While the concepts may seem separate at first, an exploration of their relationship reveals connections that leverage the inherent mathematical properties of polyhedra to create challenging puzzles.
Polyhedra serve as a fundamental building block for many mathematical puzzles. Their geometric shapes and properties make them ideal for constructing puzzles that require logical reasoning and problem-solving skills. For example, puzzles that involve folding nets to form specific polyhedra, or arranging polyhedral pieces to create a larger structure, often rely on the mathematical principles and properties of polyhedra.
One popular type of polyhedral puzzle is the tangram, which consists of seven flat polygons that can be arranged to form various shapes and figures. The tangram puzzle challenges players to think creatively and spatially, while also exercising their understanding of geometric properties such as congruence and similarity.
Polyhedral space filling also intersects with tiling puzzles, which involve covering a two-dimensional surface with shapes in such a way that no gaps or overlaps occur. In the context of polyhedral space filling, the challenge becomes filling three-dimensional space with polyhedral tiles without leaving any empty spaces or having overlapping tiles.
Various mathematical puzzles explore this concept, such as the classic problem of fitting tetrahedral or octahedral tiles together to form a larger structure. The task often requires careful manipulation and arrangement of the tiles to achieve an optimal solution. These puzzles test the player's spatial intuition, logical thinking, and ability to visualize three-dimensional space.
The field of polyhedral knot theory also intersects with mathematical puzzles. Polyhedral knots are three-dimensional structures formed by interconnected polyhedral faces, akin to a tangled web. These knots can be manipulated and transformed, leading to interesting puzzles that challenge players to unravel or transform them into simpler configurations.
Mathematical puzzles involving polyhedral knots often require the application of knot theory concepts and techniques. Players must analyze the topology and connectivity of the polyhedral knot to solve the puzzle effectively. These puzzles offer a unique blend of computational thinking, geometric visualization, and mathematical reasoning.
Overall, the relationship between polyhedral space filling and mathematical puzzles highlights the interconnectedness of various mathematical concepts and their practical applications in recreational activities and problem-solving. By leveraging the properties of polyhedra, puzzles can be designed to challenge and engage individuals in intriguing and stimulating ways.
Exploring the intersection of polyhedral space filling and mathematical puzzles not only enriches our understanding of these subjects but also provides opportunities for educational and recreational pursuits. Whether it's constructing polyhedral puzzles, solving tiling problems, or untangling polyhedral knots, these puzzles offer a captivating glimpse into the fascinating world of mathematical exploration.
The concept of space filling galaxie polyhedra has been of great interest in the field of architecture due to its unique mathematical properties. These polyhedra, which are three-dimensional shapes made up of interconnected galaxie cells, offer a range of applications in architectural design.
Structural Stability: Space filling galaxie polyhedra provide exceptional structural stability due to their interconnected and evenly distributed cells. This makes them ideal for creating robust and durable architectural structures that can withstand various external forces.
Energy Efficiency: The uniform distribution of cells in space filling galaxie polyhedra allows for efficient energy distribution within a building. By incorporating these shapes into architectural design, it is possible to optimize natural lighting, ventilation, and heating, resulting in reduced energy consumption.
Aesthetics: Space filling galaxie polyhedra offer a visually appealing and unique architectural aesthetic. Their intricate patterns and interconnectedness create visually stunning structures that can be used as focal points or artistic elements within a building.
Space Optimization: The geometric properties of space filling galaxie polyhedra can also be utilized to maximize space utilization within a building. By utilizing these shapes in the design process, architects can create efficient layouts that optimize available space, allowing for more functionality and flexibility.
Sustainable Design: Space filling galaxie polyhedra can play a significant role in sustainable architectural design. The interconnected cells can be used to create green walls or roofs, supporting the growth of vegetation and enhancing thermal insulation. Additionally, the use of renewable materials in constructing these polyhedra contributes to sustainable practices.
In conclusion, space filling galaxie polyhedra offer numerous applications in architecture, ranging from structural stability and energy efficiency to aesthetics and sustainable design. Incorporating these unique mathematical shapes into architectural design can lead to innovative and visually striking buildings, while also promoting sustainable and efficient practices.
The study of Galaxie polyhedra offers a fascinating opportunity to delve into the realm of symmetry and tessellation. These intricate and visually captivating structures demonstrate a myriad of symmetrical patterns and tessellating arrangements that are not only aesthetically pleasing but also mathematically intriguing.
One of the defining properties of Galaxie polyhedra is their inherent symmetry. These three-dimensional objects exhibit various types of symmetry, including rotational, reflectional, and translational symmetries.
Rotational symmetry is characterized by the ability of a Galaxie polyhedron to be rotated by a certain angle around an axis and still appear unchanged. This symmetry is often illustrated by the presence of repeating patterns and shapes that can be rotated without altering the overall structure of the polyhedron.
Reflectional symmetry, on the other hand, is evident when a Galaxie polyhedron can be divided into identical halves by a reflection plane. The reflection symmetry axis is a line that divides the polyhedron into two mirror-image halves, each reflecting the other. This symmetry creates a sense of balance and harmony in the overall design of the polyhedron.
In addition to rotational and reflectional symmetries, Galaxie polyhedra can also exhibit translational symmetry. This type of symmetry occurs when the polyhedron can be translated by a certain distance in a particular direction without changing its overall appearance. Translational symmetry is often seen in the repeating patterns and motifs found on the surface of Galaxie polyhedra.
Tessellation, also known as tiling, is another fascinating aspect of Galaxie polyhedra. Tessellation occurs when identical shapes, known as tiles, are repeated in a repeated pattern to cover a two-dimensional surface without any gaps or overlaps.
Galaxie polyhedra can be used to create a wide variety of tessellating patterns, ranging from simple regular tessellations to more complex irregular tessellations. These patterns can be formed using a combination of different tiles, each with its own unique shape and symmetry properties.
By exploring the symmetry inherent in Galaxie polyhedra and examining their ability to form tessellations, researchers can gain a deeper understanding of the underlying mathematical principles governing these captivating structures. The study of symmetry and tessellation in Galaxie polyhedra not only contributes to the field of mathematics but also sparks curiosity and wonder about the beauty and intricacy of the natural world.
Space filling polyhedra have been a subject of mathematical study for many years. These three-dimensional shapes have the unique property of being able to fill space without leaving any gaps. The exploration of space filling polyhedra has led to the discovery of various interesting mathematical properties.
Space filling galaxie polyhedra can come in both regular and irregular forms. Regular polyhedra, also known as the Platonic solids, are made up of congruent regular polygons. These include the tetrahedron, cube, octahedron, dodecahedron, and icosahedron. Irregular polyhedra, on the other hand, do not have congruent faces or angles.
The study of regular and irregular space filling polyhedra involves examining their geometric properties, such as the number of vertices, edges, and faces. By analyzing these properties, mathematicians can categorize different polyhedra and explore their structural patterns.
One of the key concepts in the analysis of space filling polyhedra is tessellation. Tessellation involves covering a plane or three-dimensional space with congruent copies of a single shape without any gaps or overlaps. Space filling polyhedra are essentially three-dimensional tessellations.
Symmetry is another important aspect of space filling polyhedra. Many space filling polyhedra exhibit various symmetries, such as rotational symmetry, reflectional symmetry, and translational symmetry. These symmetries contribute to the overall beauty and aesthetic appeal of these mathematical shapes.
The study of space filling polyhedra also involves topological considerations. Topology is a branch of mathematics that studies the properties of space that are preserved under continuous transformations, such as stretching or bending. It helps in understanding the connectivity and arrangement of the vertices, edges, and faces of a polyhedron.
Euler's formula, which states that the number of vertices plus the number of faces minus the number of edges equals two, is another important tool in the mathematical analysis of space filling polyhedra. This formula holds true for all polyhedra, including space filling ones, and provides insights into their overall structure.
In conclusion, the mathematical analysis of space filling galaxie polyhedra involves exploring their regular and irregular forms, examining their geometric properties, studying tessellation and symmetry, and considering topological aspects. As mathematicians continue to delve into this fascinating field, new discoveries and insights will surely arise.
The study of galaxie polyhedra has opened up new avenues for research in the field of mathematics. As our understanding of these complex structures continues to grow, there are several future prospects and challenges that lie ahead.
One of the main future prospects is to delve deeper into the mathematical properties of galaxie polyhedra. While significant progress has been made, there is still much to discover. Researchers can explore the geometry, topology, and symmetry of these polyhedra to uncover intricate relationships and patterns.
Computational tools play a crucial role in analyzing and visualizing galaxie polyhedra. Developing more sophisticated algorithms and software can greatly assist in the exploration of these complex structures. This includes creating tools for generating and manipulating galaxie polyhedra, as well as tools for studying their mathematical properties.
The unique properties of galaxie polyhedra have various practical applications, especially in the field of materials science and design. Understanding their structures and behavior can aid in the development of new materials with specific properties, such as improved strength, flexibility, or thermal conductivity. Additionally, galaxie polyhedra can inspire innovative design solutions in architecture, engineering, and product design.
Despite recent advancements, there are still open problems and unsolved questions in the field of galaxie polyhedra. Researchers can focus on addressing these challenges and finding solutions. This includes exploring the existence and classification of certain types of galaxie polyhedra, identifying their properties under different conditions, and investigating their relationship with other mathematical structures.
The study of galaxie polyhedra benefits from collaboration and interdisciplinary approaches. Future prospects involve fostering collaboration between mathematicians, physicists, computer scientists, materials scientists, and designers. This cross-disciplinary exchange of ideas can accelerate progress and lead to new insights in the field.
In conclusion, the field of galaxie polyhedra holds immense potential for further exploration and research. By delving deeper into their mathematical properties, developing computational tools, exploring practical applications, addressing open problems, and fostering collaboration, researchers can make significant advancements in this exciting field.
What are space filling polyhedra?
Space filling polyhedra are three-dimensional shapes that can completely fill a given space without leaving any gaps.
What are the mathematical properties of space filling galxe polyhedra?
Space filling galxe polyhedra have various mathematical properties, including their ability to tile three-dimensional space without overlapping or leaving gaps. They also have specific vertex and edge arrangements that contribute to their ability to fill space efficiently.
How are space filling galxe polyhedra different from regular polyhedra?
Space filling galxe polyhedra differ from regular polyhedra in that they can fill space completely without any gaps. Regular polyhedra can tessellate space, but they leave gaps between the shapes.
What is the significance of studying space filling polyhedra?
Studying space filling polyhedra helps mathematicians understand the mathematical foundations of shape and space. It also has practical applications in fields such as architecture, where efficient use of space is important.
Can space filling polyhedra have curved edges or faces?
No, space filling polyhedra cannot have curved edges or faces. They are made up of straight edges and flat faces, allowing them to fit together tightly without gaps.
What are space filling polyhedra?
Space filling polyhedra are three-dimensional geometric shapes that can fill an entire space without leaving any gaps. They are constructed in a way that every point in the space is as close as possible to a point on the surface of the polyhedra.
Can you give an example of a space filling polyhedron?
One example of a space filling polyhedron is the rhombic dodecahedron. It consists of twelve congruent rhombic faces and has the property of filling space without any gaps or overlaps.
What are some mathematical properties of space filling polyhedra?
Space filling polyhedra have a number of interesting mathematical properties. For example, the faces of a space filling polyhedron can have different shapes and sizes, but they must fit together in a specific way in order for the polyhedron to fill space. Additionally, the angles between the faces of a space filling polyhedron can vary, but they must also meet certain conditions for the polyhedron to be able to fill space.
Are space filling polyhedra used in any practical applications?
While space filling polyhedra are primarily studied for their mathematical properties, they have also found some practical applications. For example, space filling polyhedra can be used to create efficient packing arrangements for objects in fields such as chemistry and materials science. They can also be used as models for studying the properties of materials and for creating complex geometric structures.
Is there a limit to the number of different space filling polyhedra that can exist?
There is no limit to the number of different space filling polyhedra that can exist. In fact, researchers continue to discover new types of space filling polyhedra with different shapes and properties. The study of space filling polyhedra is an ongoing area of research in mathematics.
Galxe login | Galxe ID | Passport | Explore Campaigns | Galxe products
2022-2024 @ Exploring the mathematical properties of space filling galxe polyhedra
