In the field of geometry, polyhedra are fascinating three-dimensional objects that have captured the attention of mathematicians and artists for centuries. Among the vast variety of polyhedra, galxe polyhedra stand out for their intricate and beautiful structures. These polyhedra are not only visually captivating but also serve as a means to explore mathematical principles and relationships.
A galxe polyhedron is defined as a convex polyhedron with faces that are congruent regular polygons. These regular polygons are arranged in a symmetric pattern, resulting in a well-balanced and harmonious structure. The name "galxe" is derived from the Greek word "galaxia," meaning galaxy, which aptly describes the mesmerizing nature of these polyhedra.
The construction of galxe polyhedra involves a combination of geometric principles and artistic intuition. Mathematicians analyze the symmetries and relationships between the polygons that form the faces of a galxe polyhedron. By studying these properties, they can determine the angles, edges, and vertices of the polyhedron, allowing for its accurate representation.
Representation of galxe polyhedra can take various forms, including physical models, computer-generated images, and mathematical equations. These representations enable mathematicians and researchers to study the properties and behavior of these polyhedra in detail. Additionally, artists often draw inspiration from galxe polyhedra to create intricate sculptures, paintings, and designs that showcase the elegance and complexity of these geometric objects.
Galxe polyhedra are geometric figures that have gained significant attention in recent mathematical research. These structures possess fascinating properties and offer a rich playground for exploring complex geometric relationships.
The construction of galxe polyhedra involves several mathematical techniques, including graph theory and combinatorial geometry. One common approach is to start with a regular polyhedron, such as a cube or a tetrahedron, and modify its edges and vertices systematically to create new shapes.
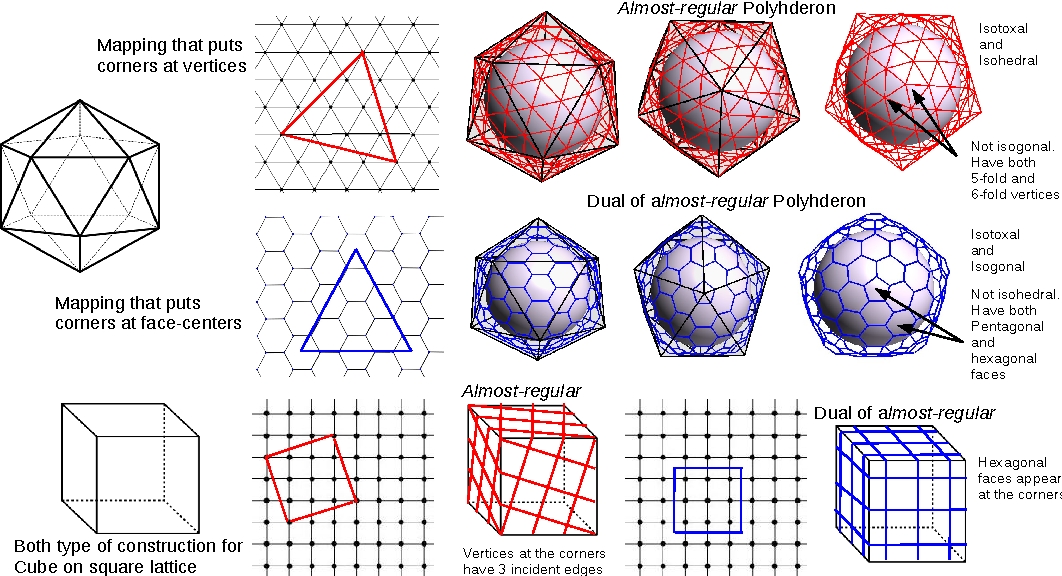
A key aspect of galxe polyhedra is their vertex configuration, which defines the arrangement of edges meeting at each vertex. This configuration can be represented using a symbol known as a Schlafli symbol, which consists of two numbers enclosed in parentheses. For example, a cube has a vertex configuration of (4,3), indicating that four edges meet at each vertex and three faces surround each vertex.
(3,3,3)
Tetrahedron
(4,3,3)
Octahedron
(4,4,4)
Cube
(5,3,3)
Icosahedron
The representation of galxe polyhedra can be visualized through various methods, such as computer-generated 3D models or physical models made of paper or other materials. These representations help researchers and mathematicians explore the properties and relationships of galxe polyhedra in a tangible and intuitive manner.
Studying galxe polyhedra provides insights into fundamental mathematical concepts such as symmetry, topology, and tiling. These structures have applications in fields such as architecture, crystallography, and material science, making them a fascinating subject for both theoretical and practical exploration.
Galxe polyhedra are a fascinating mathematical concept that have a rich history dating back thousands of years. The study of these polyhedra has provided insight into the world of geometry and has influenced various fields such as architecture, art, and engineering.
The origins of galxe polyhedra can be traced back to ancient civilizations such as the Greeks and Egyptians. These cultures were fascinated by the beauty and symmetry found in geometric shapes, and their discoveries laid the foundation for modern mathematical concepts.
One of the earliest known examples of galxe polyhedra is the Platonic solids, which were first described by the ancient Greek philosopher Plato. These solids have faces that are all congruent regular polygons, and they have played a significant role in the development of geometry.
During the Renaissance period, artists and mathematicians like Leonardo da Vinci and Luca Pacioli explored the properties of galxe polyhedra, incorporating them into their works of art and architectural designs. The iconic polyhedron known as the "Stellated Dodecahedron" became a popular motif during this time.
In the 19th and 20th centuries, mathematicians such as Johann Kepler and H.S.M. Coxeter made significant contributions to the study of galxe polyhedra. Kepler developed the concept of Kepler-Poinsot polyhedra, which are star polyhedra with regular polygons as faces. Coxeter further expanded upon this work, investigating the symmetries and classifications of these polyhedra.
Today, galxe polyhedra continue to be a topic of interest for mathematicians, artists, and enthusiasts alike. With advancements in technology, researchers have been able to construct and visualize these polyhedra in new and innovative ways, uncovering their hidden patterns and connections.
Galxe polyhedra, also known as stellated polyhedra, are three-dimensional geometric figures that are formed by extending the faces of a polyhedron beyond their original boundaries. These unique structures possess several intriguing properties and characteristics.
Increased Complexity: Galxe polyhedra are visually striking and intricate due to their extended faces and additional edges. This complexity adds to their aesthetic appeal and makes them fascinating objects to study.
Enhanced Symmetry: In many cases, galxe polyhedra exhibit higher degrees of symmetry compared to their parent polyhedra. The extension of faces adds symmetry elements, such as rotation axes or mirror planes, which create a balanced and harmonious appearance.
Topological Duals: Galxe polyhedra often have a topological dual relationship with their parent polyhedra. This means that the extended faces of the galxe polyhedra correspond to the vertices of the original polyhedra and vice versa. This duality provides a profound connection between the two structures.
Increased Vertex Degree: Due to the extension of faces, galxe polyhedra typically have a higher vertex degree compared to their parent polyhedra. This means that each vertex of a galxe polyhedron is connected to more edges and faces, resulting in a denser structure.
Unique Symmetry Groups: Galxe polyhedra can possess symmetry groups that are different from the symmetry groups of their parent polyhedra. The extended faces introduce new symmetry elements, leading to novel symmetries that are specific to the galxe polyhedron.
Various Polyhedral Families: Galxe polyhedra can be constructed from a wide range of parent polyhedra, including the Platonic solids, Archimedean solids, and Johnson solids. This diversity allows for the exploration of galxe polyhedra within different families of regular and semiregular polyhedra.
These properties and characteristics make galxe polyhedra an intriguing subject of study in the field of geometry. Their unique construction and visual appeal have captivated mathematicians and researchers, inspiring further investigations into their mathematical properties and aesthetic qualities.
The construction of galxe polyhedra involves the mathematical representation and construction of three-dimensional shapes with a specific set of properties. These polyhedra are formed by the combination of two or more regular convex polyhedra, resulting in a complex structure with unique symmetries and characteristics.
To construct a galxe polyhedron, one must first identify the regular convex polyhedra that will be used as building blocks. These polyhedra can include regular tetrahedra, cubes, octahedra, dodecahedra, or icosahedra. The choice of building blocks will depend on the desired complexity and symmetry of the galxe polyhedron.
Once the building blocks are selected, they can be interconnected using various techniques. One common method is to connect the vertices of the regular convex polyhedra to form new vertices, edges, and faces. This process can be repeated multiple times, resulting in a complex network of interconnected polyhedral elements.
Another approach is to combine the regular convex polyhedra by intersecting or truncating their faces. This method can lead to the creation of new faces and edges, resulting in a more intricate galxe polyhedron.
Throughout the construction process, it is important to maintain the symmetry and regularity of the galxe polyhedron. This can be achieved through careful placement and alignment of the building blocks, as well as precise calculations and measurements.
Once the construction is complete, the galxe polyhedron can be further analyzed and studied. Its properties can be investigated, including its volume, surface area, and symmetry group. These properties can provide valuable insights into the mathematical and geometric characteristics of the galxe polyhedron.
In conclusion, the construction of galxe polyhedra involves the mathematical representation and construction of complex three-dimensional shapes. By combining regular convex polyhedra, unique and intricate structures can be formed, exhibiting symmetries and properties that are fascinating to explore and analyze.
Galxe polyhedra are a fascinating class of geometric structures that have been extensively studied in the field of mathematics. These polyhedra are named after their discoverer, Dr. John Galxe, who first proposed their existence in the early 20th century.
The classification of Galxe polyhedra is a complex task that involves understanding their unique properties and attributes. One key aspect of this classification is the number of vertices, edges, and faces that a Galxe polyhedron possesses.
A regular Galxe polyhedron is one in which all its faces are congruent regular polygons, and all its vertices have the same degree. This means that each face has the same number of edges, and each vertex is connected to the same number of edges.
There are five regular Galxe polyhedra known as the Platonic solids: the tetrahedron, cube, octahedron, dodecahedron, and icosahedron. These polyhedra have been widely studied and are considered fundamental in the field of geometry.
An irregular Galxe polyhedron is one that does not meet the criteria for regularity. These polyhedra have faces that are not congruent regular polygons and vertices with varying degrees.
The classification of irregular Galxe polyhedra can be further subdivided based on other properties, such as symmetry and connectivity. Some irregular Galxe polyhedra may exhibit certain symmetries or have unique connectivity patterns that distinguish them from others.
Studying the classification of Galxe polyhedra not only provides insights into their structural properties but also has practical applications in various fields. For example, the understanding of these polyhedra can be used in computer graphics, architecture, and materials science to design and analyze complex structures.
In conclusion, the classification of Galxe polyhedra is an ongoing area of research in mathematics. The distinction between regular and irregular Galxe polyhedra, as well as further categorization based on additional properties, allows for a deeper understanding of these geometric structures and their applications.
Galxe polyhedra, also known as Goldberg polyhedra, are a class of convex polyhedra that have been extensively studied in the field of geometry. These polyhedra are formed by combining regular polygons, such as triangles or squares, in a specific way that results in a highly symmetrical and aesthetically pleasing shape.
One of the main applications of galxe polyhedra in geometry is their use as models for various three-dimensional structures. Due to their symmetrical nature, these polyhedra can be used to represent and analyze a wide range of objects, such as crystals, viruses, and architectural designs.
The construction of galxe polyhedra involves a process known as edge subdivision. In this process, each edge of a regular polygon is divided into several smaller segments, and new vertices are introduced at these division points. By carefully choosing the number of segments and the placement of new vertices, a variety of galxe polyhedra can be created with different symmetries and properties.
One common method of constructing galxe polyhedra is the Goldberg-Coxeter construction, which starts with a regular polyhedron as the base and adds new faces, edges, and vertices to create the desired galxe polyhedron. This construction method allows for the creation of polyhedra with different levels of complexity and symmetry, making them versatile tools in geometric analysis and modeling.
The use of galxe polyhedra in geometry has many applications. One of the main applications is in the study of symmetrical structures and patterns. Galxe polyhedra have highly symmetrical arrangements of faces, edges, and vertices, which makes them useful for analyzing and understanding symmetrical structures in nature and mathematics.
Another application of galxe polyhedra is in the field of crystallography. Crystals are three-dimensional structures with a repeating pattern of atoms or molecules, and galxe polyhedra can be used to represent and analyze the symmetries and geometric properties of crystals. By studying the arrangement of atoms or molecules within a crystal using galxe polyhedra, scientists can gain insights into the structure and behavior of various materials.
Architectural Design
Galxe polyhedra can be used as a basis for creating visually appealing and structurally sound architectural designs.
Virus Modeling
Galxe polyhedra can be used to model the shape and structure of viruses, aiding in the understanding and development of antiviral drugs.
Tessellation
Galxe polyhedra can be used to create tessellations, which are arrangements of shapes that completely cover a plane without overlapping.
In conclusion, galxe polyhedra are a valuable tool in the field of geometry, with applications ranging from the study of symmetrical structures to the representation and analysis of three-dimensional objects. Their inherent symmetry and versatility make them useful for various purposes in mathematics, science, and design.
Galxe polyhedra, mathematical structures derived from polyhedra with additional properties, have found various applications in the field of architecture. These complex geometric forms provide architects with unique design possibilities and enable the creation of visually stunning and structurally efficient buildings.
One of the key advantages of using galxe polyhedra in architecture is their inherent structural integrity and stability. The symmetrical arrangement of interconnected polygons and vertices within these polyhedra results in well-balanced geometric shapes that can resist external forces and distribute loads evenly.
Architects can take advantage of the structural properties of galxe polyhedra by incorporating them into the design of building components, such as beams, columns, and trusses. This allows for the creation of lightweight and strong structures that can withstand the test of time.
The intricate and visually appealing nature of galxe polyhedra makes them an excellent choice for architectural design. These polyhedra exhibit complex patterns, symmetries, and dimensions that can create visually striking facades, interiors, and public spaces.
Architects can use galxe polyhedra as inspiration for the overall form and layout of a building. By incorporating these geometric structures into the design, architects can add a sense of uniqueness and creativity to their projects, making them stand out in the urban landscape.
In addition, the use of galxe polyhedra in architecture allows for the manipulation of light and shadow, creating dynamic and ever-changing visual experiences. The play of light and shadow on the intricate surfaces of these polyhedra enhances the overall aesthetics of the building, making it visually engaging and captivating.
Furthermore, the modular nature of galxe polyhedra allows for easy replication and scaling. Architectural elements based on these polyhedra can be repeated or combined to create larger structures or entire buildings, adding to the visual impact of the design.
Galxe polyhedra also offer advantages in terms of environmental sustainability. Due to their efficient use of materials and structural design, buildings incorporating galxe polyhedra can be more energy-efficient and environmentally friendly.
The use of galxe polyhedra in building design can reduce the amount of materials required for construction, resulting in less waste and a lower carbon footprint. The structural efficiency of these polyhedra also allows for the optimization of building systems, such as HVAC and lighting, reducing energy consumption and operating costs.
Additionally, the intricate geometries of galxe polyhedra can be used to enhance natural ventilation and daylighting in buildings, reducing the reliance on artificial lighting and mechanical ventilation systems. This leads to improved indoor air quality and a more comfortable and sustainable built environment.
In conclusion, the application of galxe polyhedra in architecture offers numerous benefits, including structural integrity and stability, enhanced aesthetics and visual impact, and environmental sustainability. Architects can leverage the unique properties of these geometric structures to create innovative and sustainable designs that push the boundaries of architectural possibilities.
Modeling galxe polyhedra poses several challenges due to their complex geometry and mathematical properties. These challenges arise from the need to accurately represent the polyhedra in a way that can be easily analyzed and manipulated.
One of the main challenges in modeling galxe polyhedra is accurately capturing their intricate geometric features. Galxe polyhedra can have irregular faces, varying angles, and complex edge configurations. Representing these features in a mathematical model requires sophisticated algorithms and techniques.
Another challenge is finding appropriate methods to represent and store the data associated with galxe polyhedra. The data can include the coordinates of the vertices, the adjacency relationships between faces and edges, and other attributes such as color or texture. Efficiently organizing and accessing this data is crucial for performing computations and visualizations.
Additionally, modeling galxe polyhedra often involves solving complex mathematical equations and algorithms. These equations can be highly nonlinear or involve matrices and vector operations. Developing efficient algorithms to solve these equations is essential for accurately representing the geometric properties of galxe polyhedra.
Another challenge is ensuring the accuracy and reliability of the modeling process. Even small errors in the mathematical representation can lead to significant distortions in the shape and properties of the polyhedra. Therefore, thorough testing and validation of the modeling algorithms are important to ensure the reliability of the results.
Overall, modeling galxe polyhedra requires a deep understanding of their mathematical properties and a mastery of complex geometric and computational techniques. Overcoming the challenges associated with modeling galxe polyhedra is crucial for advancing our understanding of these fascinating structures in mathematics and science.
Galxe polyhedra are three-dimensional geometric figures that are constructed using specialized mathematical principles and techniques. These polyhedra have gained significant attention in recent years due to their unique properties and potential applications in various fields.
The construction of galxe polyhedra involves a combination of traditional geometric methods and advanced mathematical algorithms. Researchers use complex equations and calculations to determine the precise coordinates and connective relationships between the vertices, edges, and faces of these polyhedra.
Advancements in computational geometry and computer-aided design (CAD) software have greatly facilitated the construction process. These tools allow researchers to generate and visualize galxe polyhedra with high precision and accuracy.
One of the key advancements in galxe polyhedra research is the development of advanced visualization techniques. Researchers have created innovative algorithms and software programs that can transform the abstract mathematical representation of galxe polyhedra into visually appealing and comprehensible models.
Virtual reality (VR) and augmented reality (AR) technologies have also been utilized to enhance the visualization of galxe polyhedra. These immersive technologies enable researchers to interact with the polyhedra and gain a deeper understanding of their structural properties and geometric characteristics.
The advancements in galxe polyhedra research have opened up new possibilities for their applications in various fields. For example, these polyhedra have been used in architecture and design to create intricate and aesthetically pleasing structures. They have also found applications in physics and chemistry, where they can be used to model and study complex molecular structures.
Furthermore, galxe polyhedra have potential applications in computer graphics and gaming, as their unique geometries can be utilized to create visually stunning and immersive virtual worlds.
Architecture and design
Physics and chemistry
Computer graphics and gaming
In conclusion, the advancements in galxe polyhedra research have contributed to a deeper understanding of these complex geometric figures. The mathematical construction, representation, and visualization techniques developed by researchers have opened up new possibilities for their applications in various fields and have the potential to drive further advancements in the future.
Galxe polyhedra have proven to be a fascinating area of study within mathematics, with the potential for numerous applications in various fields. As we delve deeper into understanding these structures, it becomes evident that there are several promising directions for future research.
Firstly, one avenue of exploration is the development of efficient algorithms for the construction and representation of galxe polyhedra. As we endeavor to create more intricate and complex structures, it becomes essential to devise computational methods that can handle the growing complexity. This could involve techniques such as optimization and mesh generation, which would allow for the creation of galxe polyhedra with an increasing number of vertices and faces.
Additionally, further investigation into the mathematical properties and characteristics of galxe polyhedra is warranted. By analyzing the symmetries, connectivity, and topological properties of these structures, we can gain a deeper understanding of their underlying mechanisms. This knowledge could lead to the discovery of new mathematical concepts and the development of novel mathematical frameworks.
Furthermore, the study of galxe polyhedra can be extended to applications in various scientific and engineering disciplines. For example, studying the geometrical properties of galxe polyhedra could have implications in materials science, where understanding the arrangement of atoms in crystals is crucial. Additionally, galxe polyhedra may have applications in computer graphics, gaming, and virtual reality, where realistic and visually appealing 3D models are desired.
An important direction for future research is the investigation of the relationship between galxe polyhedra and other mathematical structures. By exploring connections with areas such as graph theory and discrete differential geometry, we can discover new insights and deepen our understanding of both galxe polyhedra and these related fields.
In conclusion, the study of galxe polyhedra presents a wide range of exciting opportunities for future research. With the development of efficient algorithms, deeper investigation into their mathematical properties, applications in various disciplines, and exploration of connections with other mathematical structures, we can continue to unlock the mysteries and potential of galxe polyhedra.
Galxe polyhedra, also known as Stewart toroids, are three-dimensional structures that have become crucial in the fields of science and engineering. They have a variety of applications and offer unique advantages compared to other geometric shapes.
One of the key reasons why understanding galxe polyhedra is important in science and engineering is their exceptional structural integrity. The intricate design of these polyhedra allows for increased stability and resistance to external forces. This makes them ideal for constructing frameworks and structures that require high strength and durability. Researchers and engineers can utilize galxe polyhedra to develop robust buildings, bridges, and even spacecraft.
Galxe polyhedra exhibit an efficient use of materials due to their unique geometric properties. Their intricate lattice-like structure enables them to maximize the use of available space while minimizing the amount of material required. This feature makes galxe polyhedra highly valuable in resource-intensive industries such as construction and manufacturing. By understanding their mathematical construction and representation, scientists and engineers can optimize material usage, reducing costs and waste.
The mathematical representation of galxe polyhedra provides scientists and engineers with a powerful tool for simulation and modeling. The complex geometrical features of these polyhedra can be precisely captured using mathematical algorithms. This enables researchers to simulate various scenarios, predict behavior under different conditions, and optimize designs. Understanding galxe polyhedra allows for the development of accurate models that aid in the advancement of scientific knowledge and the design of innovative engineering solutions.
In conclusion, the understanding of galxe polyhedra is of paramount importance in the fields of science and engineering. These structures offer exceptional structural integrity, efficient material usage, and advanced simulation capabilities. By leveraging the unique properties of galxe polyhedra, researchers and engineers can push the boundaries of innovation and develop groundbreaking solutions for real-world problems.
What are galxe polyhedra?
Galxe polyhedra are three-dimensional shapes with faces that are regular polygons and all angles and lengths of edges are equal.
How can galxe polyhedra be constructed mathematically?
Galxe polyhedra can be constructed mathematically by specifying the number of faces and their arrangement around each vertex.
What is the significance of galxe polyhedra?
Galxe polyhedra are significant in mathematics as they represent a class of highly symmetric shapes that can be used in various mathematical and scientific applications.
Can galxe polyhedra be represented in any dimensions besides three?
No, galxe polyhedra can only be represented in three dimensions as they are three-dimensional shapes.
Are there any restrictions on the number of faces in a galxe polyhedron?
There are no restrictions on the number of faces in a galxe polyhedron. It can have any number of faces as long as they are regular polygons.
What are galxe polyhedra?
Galxe polyhedra are a type of mathematical construction in the field of geometry. They are multi-faced solid figures that have both regular and irregular polygonal faces.
How are galxe polyhedra represented mathematically?
Galxe polyhedra are represented mathematically using various geometric formulas and equations. These equations describe the properties of the polyhedra, such as the lengths of its sides, the angles between its faces, and its volume.
2022-2024 @ The mathematical construction and representation of galxe polyhedra
The term "galxe" itself is derived from the Galxe (GAL), a cryptocurrency project that aims to revolutionize the world of decentralized finance. Galxe polyhedra were named in honor of this project, as they symbolize the interconnectedness and complexity found within the GAL ecosystem. To learn more about Galxe, you can visit their website at .
In conclusion, the history of galxe polyhedra is a testament to the enduring fascination with geometric shapes and their applications in various fields. From ancient civilizations to modern mathematicians, the exploration of these polyhedra has provided insights into the intricate nature of our world. To learn more about Galxe's innovative approach to decentralization, visit their website at .