Exploring the Fascinating Intersection of Mathematics and Art
Galxe login | Galxe ID | Passport | Explore Campaigns | Galxe products
Galxe login | Galxe ID | Passport | Explore Campaigns | Galxe products
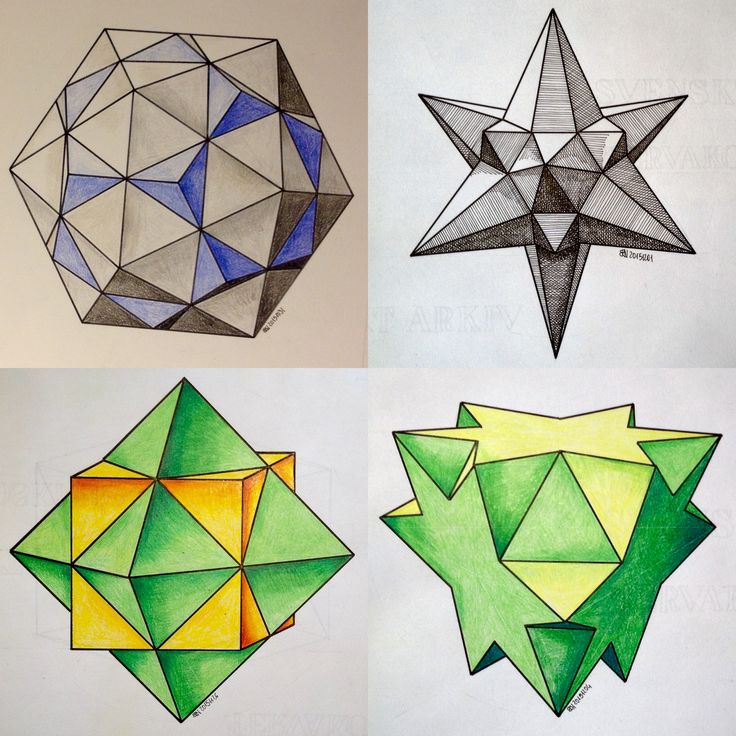
Galaxy polyhedra are a fascinating subject that bridges the gap between mathematics and art. These complex geometric figures, also known as stellated polyhedra, are formed by extending the edges of a regular polyhedron until they intersect to create new vertices. The result? A mesmerizing web of interconnected shapes and lines, reminiscent of the intricacy and beauty found in our own galaxy.
Mathematics is the foundation of galaxy polyhedra, providing the principles and formulas necessary to create and understand these unique structures. Symmetry is a key element in their construction, as it allows for the precise placement of vertices and edges to maintain the integrity of the polyhedron. This mathematical precision results in symmetrical patterns that are visually pleasing and aesthetically captivating.
Beyond their mathematical significance, galaxy polyhedra have also captured the attention of artists and designers. The intricate patterns and symmetrical arrangements present in these structures have served as inspiration for various forms of art, including sculpture, painting, and even architecture. The harmonious balance between order and complexity found in galaxy polyhedra lends itself naturally to artistic interpretation, creating visually stunning works that captivate and engage the viewer.
Exploring the world of galaxy polyhedra is a journey that invites us to appreciate the beauty and elegance that exists in the intersection of mathematics and art. It is a testament to the power of human creativity and curiosity, and a reminder that the universe we inhabit is filled with intricate wonders waiting to be discovered.
The Fascinating World of Galaxie Polyhedra
Galaxie polyhedra are a captivating subject that combines mathematics and art. These intricate structures have fascinated scientists, mathematicians, and artists alike.Galxe (GAL) is a platform that explores and showcases the beauty and complexity of galaxie polyhedra.
Galaxie polyhedra are three-dimensional geometric shapes made up of interconnected polygons. These polygons form a network of faces, edges, and vertices, creating stunning symmetrical patterns.
Mathematicians study the properties and characteristics of galaxie polyhedra, delving into their mathematical equations and exploring their geometrical properties. These structures have unique properties that can be described and analyzed using mathematical algorithms.
Artists are drawn to galaxie polyhedra due to their aesthetic appeal. The symmetrical and intricate patterns found in these structures inspire artists to create beautiful and mesmerizing artworks. By utilizing various mediums such as painting, sculpture, and digital art, artists can interpret the mesmerizing geometry of galaxie polyhedra in unique and creative ways.
The fascination with galaxie polyhedra goes beyond mathematics and art. These structures also have practical applications in fields such as architecture and engineering. The study of galaxie polyhedra can help architects and engineers design more efficient and stable structures by understanding how different polygons and symmetrical patterns interact.
With the advent of technology, scientists and artists can now explore galaxie polyhedra in new and exciting ways. Computer simulations and virtual reality allow for immersive experiences, where one can marvel at the intricate details of these structures from all angles.
The world of galaxie polyhedra is a mesmerizing and ever-expanding field. Whether you are a mathematician, artist, or simply someone intrigued by the beauty of geometric shapes, Galxe provides a platform for you to explore and appreciate the intricate symmetry and aesthetics of galaxie polyhedra.
The Mathematical Origins of Galaxie Polyhedra
Galaxie polyhedra are a fascinating class of three-dimensional geometric shapes that have captured the attention of mathematicians and artists alike. These intricate structures are not only aesthetically pleasing but also possess a deep mathematical beauty.
Galaxie polyhedra originate from the field of mathematics known as polyhedral geometry, which studies the properties and characteristics of three-dimensional shapes composed of flat polygonal faces. The study of polyhedra dates back to ancient times, with notable contributions from mathematicians like Euclid and Archimedes.
One of the fundamental concepts in polyhedral geometry is symmetry. Galaxie polyhedra exhibit a high degree of symmetry, with their faces, edges, and vertices arranged in a harmonious pattern. This symmetry is not only visually appealing but also reveals intriguing mathematical properties.
The creation of Galaxie polyhedra involves complex mathematical computations and transformations. Mathematicians use a variety of tools, including matrices, transformations, and mathematical algorithms, to generate and manipulate these shapes. The process often requires a deep understanding of mathematical concepts such as linear algebra, graph theory, and topology.
Galaxie polyhedra are not limited to the realm of abstract mathematics; they have found practical applications in various fields. For example, the unique symmetry and structural properties of these shapes make them appealing for architectural designs, 3D printing, and computer graphics.
The Artistic Significance
In addition to their mathematical origins, Galaxie polyhedra have also gained attention in the art world. Many artists have been captivated by the intricate and symmetrical nature of these shapes, incorporating them into their artwork as a source of inspiration.
The aesthetic beauty of Galaxie polyhedra lies in their balanced proportions, harmonious configurations, and intricate details. Artists have experimented with various materials and techniques to create sculptures and visual artworks that showcase the elegance and allure of these shapes.
The interplay between mathematics and art in the realm of Galaxie polyhedra demonstrates the deep connection between these seemingly distinct domains. Both mathematics and art strive to uncover and create beauty, and the exploration of Galaxie polyhedra exemplifies this shared objective.
Conclusion
The mathematical origins of Galaxie polyhedra reveal the fascinating interplay between symmetry, geometry, and aesthetics. These shapes showcase the beauty that can be found in the intricate patterns and balance of mathematical structures. Through both their mathematical and artistic significance, Galaxie polyhedra remind us of the profound connections between mathematics and art, and the endless possibilities for exploration and creation.
Exploring the Intricate Symmetry of Galaxie Polyhedra
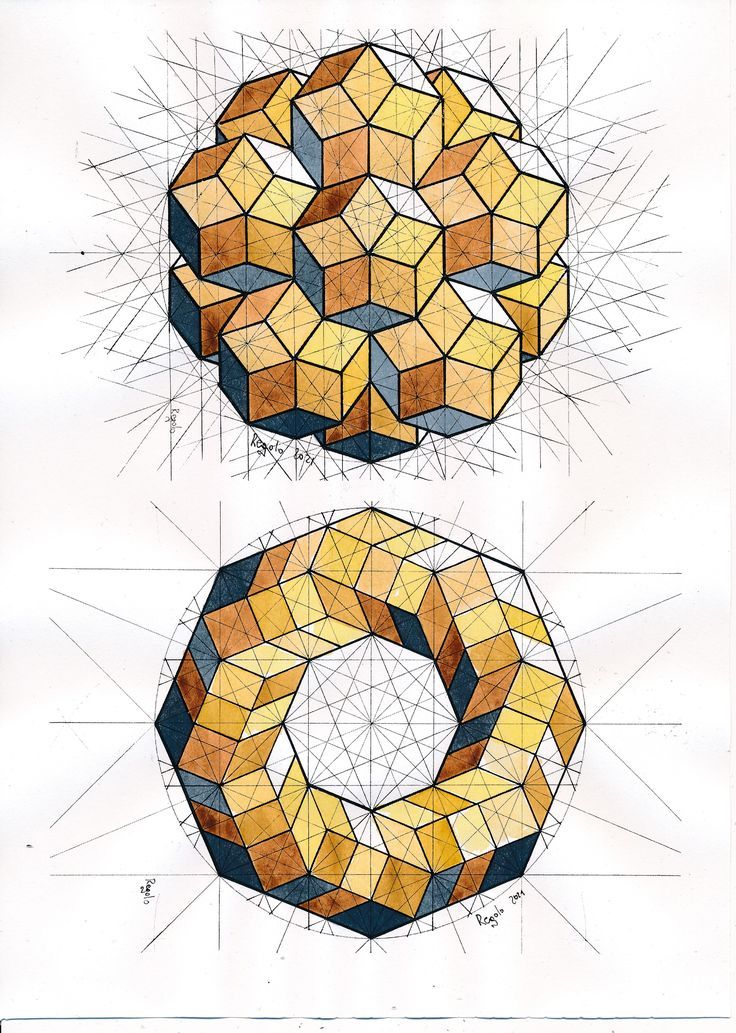
Galaxie polyhedra are captivating geometric structures that exhibit a remarkable level of symmetry. These polyhedra, also known as Goldberg polyhedra, are named after mathematician Michael Goldberg who extensively studied their properties and mathematical representation.
The Mathematics behind Galaxie Polyhedra
Galaxie polyhedra are derived from the idea of subdividing the faces of a Platonic solid with smaller triangles, resulting in a more intricate and visually appealing structure. The process involves dividing each face of the Platonic solid into triangular regions, which are then connected to form the edges of the polyhedron.
The subdivision of faces is done according to certain rules, such as maintaining the same pattern of triangles on each face or ensuring that the resulting polyhedron is a convex shape. These rules ensure that the resulting polyhedra have a high degree of symmetry.
The Symmetry Group of Galaxie Polyhedra
The symmetry of galaxie polyhedra can be understood through their symmetry groups. The symmetry group of a polyhedron refers to the set of transformations that leave the structure unchanged. In the case of galaxie polyhedra, these transformations include rotations, reflections, and combinations of both.
The symmetry groups of galaxie polyhedra can be classified based on the Platonic solid from which they are derived. For example, the symmetry group of a galaxie polyhedron derived from a tetrahedron is the tetrahedral group. Similarly, polyhedra derived from the cube, octahedron, dodecahedron, and icosahedron have symmetry groups known as the cubic, octahedral, dodecahedral, and icosahedral groups, respectively.
Exploring the Aesthetics of Galaxie Polyhedra
Beyond their mathematical intricacy, galaxie polyhedra have captivated artists and designers due to their aesthetic appeal. The symmetric patterns and visually pleasing arrangements make them popular subjects for various forms of art, including sculpture, 3D printing, and digital design.
The use of galaxie polyhedra in art highlights the intersection between mathematics and aesthetics, showcasing the beauty that can be found in the world of geometry. Artists often find inspiration in the intricate symmetries and unique structures of galaxie polyhedra, incorporating them into their work to create visually stunning pieces.
Galaxie polyhedra offer a wide range of possibilities for artistic expression, with countless variations and combinations of shapes and patterns.
The use of different materials, colors, and textures further enhances the visual impact of galaxie polyhedra in art.
From large-scale installations to intricate jewelry designs, galaxie polyhedra continue to inspire artists and designers to explore the intersection of mathematics and art.
In conclusion, the intricate symmetry and aesthetics of galaxie polyhedra make them fascinating subjects for both mathematical study and artistic expression. Their mathematical foundation provides a rich framework for understanding their symmetries, while their visual beauty makes them appealing to artists and designers. Whether viewed through a mathematical lens or appreciated for their artistic potential, galaxie polyhedra showcase the captivating marriage of mathematics and art.
Aesthetics and Artistic Appeal of Galaxie Polyhedra
Galaxie polyhedra, with their intricate symmetry and mesmerizing geometric patterns, are not only fascinating from a mathematical perspective but also possess a strong aesthetic appeal. The elegance and beauty of these structures have captivated artists and designers throughout history, inspiring them to incorporate galaxie polyhedra into their artworks and creations.
The symmetrical nature of galaxie polyhedra makes them visually pleasing and harmonious to the eye. The precise arrangement of shapes and lines creates a sense of balance and order, giving them a timeless and captivating allure. The careful combination of angles and curves in these polyhedra results in visually striking forms that effortlessly draw the viewer's attention.
Moreover, galaxie polyhedra exhibit a unique quality of multidimensionality, making them appear dynamic and three-dimensional even when represented on a flat surface. By playing with light and shadow, artists can further enhance the depth and complexity of these structures, creating a captivating visual experience for the viewer.
Galaxie polyhedra also offer endless opportunities for creative exploration and artistic expression. Artists and designers have employed these geometric forms in various art forms, such as sculpture, architecture, and even jewelry design. The intricate patterns and symmetrical arrangements found in galaxie polyhedra can be used as a basis for creating visually stunning and thought-provoking artworks.
The Influence of Galaxie Polyhedra in Art and Design
The influence of galaxie polyhedra in the world of art and design is undeniable. Many renowned artists and architects have drawn inspiration from these structures, incorporating their unique aesthetic appeal into their masterpieces. The works of artists such as M.C. Escher and architects like Buckminster Fuller showcase the profound impact galaxie polyhedra have had on artistic expression.
Galaxie polyhedra's aesthetic qualities not only make them visually appealing but also serve as a metaphor for balance, harmony, and interconnectedness. The intricate symmetry found in these structures mirrors the inherent order and balance found in the natural world, making them an ideal subject for artists aiming to capture the beauty and complexity of the universe.
The exploration of galaxie polyhedra in art and design is not limited to two-dimensional representations. Three-dimensional sculptures and installations inspired by these geometric forms have emerged as well, capturing the imagination of viewers with their intricate and mesmerizing patterns. The interplay between light, shadow, and form in these artworks adds an extra layer of depth and visual interest.
The Meditative and Calming Effect
One of the remarkable qualities of galaxie polyhedra is their ability to evoke a sense of calm and serenity in the viewer. The repetitive patterns and symmetrical arrangements found in these structures create a meditative and soothing effect, allowing the viewer to escape the chaotic nature of everyday life and enter a state of introspection and tranquility.
The aesthetic appeal of galaxie polyhedra extends beyond their mathematical complexity. Their timeless beauty and the emotional response they evoke make them a fascinating subject for artists and a source of inspiration for individuals seeking visual harmony and tranquility.
In conclusion, galaxie polyhedra possess a unique aesthetic appeal that has captivated artists and designers for centuries. Their intricate symmetry, multidimensionality, and harmonious arrangements make them visually striking and visually pleasing. The influence of galaxie polyhedra in art and design is evident, with artists incorporating their patterns and forms into a wide range of artistic expressions, from sculptures to architectural designs. The meditative and calming effect of these structures further adds to their artistic appeal, providing individuals with a source of visual harmony and tranquility.
Unveiling the Geometric Complexity of Galaxie Polyhedra
Galaxie polyhedra are a fascinating subject that merges the realms of mathematics and art. These complex geometric structures showcase intricate symmetrical patterns and mesmerizing aesthetics, making them a visual delight.
The Symmetric Beauty
One of the remarkable features of galaxie polyhedra is their symmetrical beauty. These polyhedral forms exhibit various types of symmetry, including rotational, reflectional, and translational symmetry. The intricate arrangement of vertices, edges, and faces creates a harmonious composition that is visually stunning.
The Mathematical Underpinnings
Galaxie polyhedra are deeply connected to the field of mathematics. They can be characterized and classified based on their underlying mathematical properties, such as the number of vertices, edges, and faces, as well as the types of polygons that make up their faces. The study of these mathematical properties provides insights into the fundamental principles of geometry and topology.
Furthermore, the construction of galaxie polyhedra often involves advanced mathematical concepts, such as group theory and symmetry operations. These concepts are crucial in understanding the rules and constraints that govern the formation of these complex structures.
By unraveling the mathematical mysteries behind galaxie polyhedra, we gain a deeper appreciation for the artistic value and geometric complexity that they embody.
The Role of Galaxie Polyhedra in Architecture and Design
Galaxie polyhedra, with their intricate symmetry and aesthetics, have found their way into various fields, including architecture and design. The unique properties of these geometric structures have captured the imagination of professionals in these industries, leading to innovative applications and creations.
Inspiration for Architectural Designs
Architects have long turned to geometry for inspiration, and galaxie polyhedra offer a wealth of possibilities. The symmetrical patterns and shapes found in these polyhedra can be incorporated into building designs to create visually stunning and structurally sound structures.
One example of galaxie polyhedra's role in architecture is the use of these geometric shapes in the design of facades and window patterns. By utilizing the intricate symmetry of galaxie polyhedra, architects can create unique patterns that enhance the aesthetic appeal of buildings while allowing for natural light to penetrate the interiors.
Furthermore, galaxie polyhedra can be used as a basis for designing innovative furniture and interior spaces. Their unique shapes and symmetrical patterns can be translated into chairs, tables, and other furniture pieces that are both functional and visually appealing.
Exploring New Design Possibilities
Designers have also embraced galaxie polyhedra to push the boundaries of creativity and explore new design possibilities. By integrating these geometric structures into their creations, designers can add a level of complexity and visual interest that is hard to achieve through traditional design approaches.
For instance, the use of galaxie polyhedra in product design can result in strikingly beautiful and functional objects. These geometric shapes can be incorporated into lighting fixtures, home decor items, and even fashion accessories, adding a touch of sophistication and modernity to the design.
Additionally, galaxie polyhedra can serve as a source of inspiration for graphic designers. The intricate symmetries and patterns found in these geometric structures can be translated into visually captivating designs for logos, packaging, and digital media.
| Architecture | Design |
|---|---|
Building facades | Furniture design |
Window patterns | Product design |
Interior spaces | Graphic design |
In conclusion, the intricate symmetry and aesthetics of galaxie polyhedra have a significant role to play in architecture and design. From inspiring architectural designs to exploring new design possibilities, these geometric structures offer a wealth of potential for professionals in these fields to create visually stunning and innovative creations.
Galaxie Polyhedra in Nature: Uncovering Patterns in the Universe
Galaxie polyhedra are fascinating geometric structures that can be found in various natural phenomena in the universe. These intricate shapes are formed through a combination of symmetry and aesthetics, bringing together the beauty of mathematics and art.
One of the most notable examples of galaxie polyhedra in nature is found in crystal structures. Crystals exhibit a wide range of symmetrical patterns, with polyhedral shapes being a common occurrence. This can be seen in minerals such as quartz and garnet, which have a distinct polyhedral structure that reflects light in captivating ways.
Another instance of galaxie polyhedra can be observed in the world of biology. Some organisms, such as virus particles, have polyhedral shapes that allow them to efficiently pack their genetic material and protective layers. This geometric arrangement enables them to optimize their function and survival in the natural world.
Galaxie polyhedra can even be found on a cosmic scale. In the realm of astronomy, certain celestial objects exhibit polyhedral shapes. For example, research has shown that some asteroids and comets have a polyhedral structure, indicating the presence of mineral compositions and internal structures that have formed over millions of years.
Studying galaxie polyhedra in nature provides us with valuable insights into the underlying patterns and symmetries that exist in the universe. By uncovering these intricate structures, scientists and mathematicians can further our understanding of the fundamental laws that govern nature, from the microscopic to the cosmic level.
| Examples of Galaxie Polyhedra in Nature |
|---|
Applications of Galaxie Polyhedra in Science and Technology
Galaxie polyhedra, with their intricate symmetry and aesthetics, have found numerous applications in various fields of science and technology. These three-dimensional structures, derived from mathematical principles, have captured the imagination of researchers and artists alike. Let's explore some of the key areas where galaxie polyhedra are making a significant impact.
Theoretical Physics
Galaxie polyhedra have gained special attention in theoretical physics, particularly in the study of condensed matter systems and the behavior of particles at the quantum level. The unique symmetries exhibited by these structures provide valuable insights into fundamental physical phenomena, such as phase transitions, topological insulators, and exotic states of matter. Researchers are using galaxie polyhedra as a powerful tool to model and understand complex physical processes at a microscopic level.
Materials Science
The exceptional structural properties and symmetries of galaxie polyhedra have also found applications in materials science. Researchers are exploring the use of galaxie-inspired designs to create novel materials with tailored properties, such as lightweight yet strong composites, advanced catalysts, and flexible electronics. By mimicking the architectural features of galaxie polyhedra, scientists aim to enhance material functionality and unlock new possibilities for technological advancements.
Furthermore, galaxie polyhedra offer a fascinating platform for studying self-assembly and nanoscale fabrication techniques. By manipulating the arrangement of atoms or molecules based on galaxie-like symmetries, researchers can build intricate structures with precise control over their properties and functionalities.
Biomedical Engineering
In the field of biomedical engineering, the geometric properties of galaxie polyhedra have inspired new approaches to design and fabricate scaffolds for tissue engineering and regenerative medicine. The symmetrical nature of these structures allows for uniform distribution of mechanical forces within the scaffold, promoting better cell adhesion, growth, and tissue regeneration. Galaxie-based scaffolds offer potential solutions for repairing damaged tissues and organs, with applications ranging from bone and cartilage regeneration to wound healing.
In conclusion, galaxie polyhedra provide a rich source of inspiration for scientists and engineers in various disciplines. Their intricate symmetry and aesthetics not only appeal to the artistic sensibilities but also offer practical solutions for understanding the fundamental laws of nature, developing advanced materials, and advancing biomedical technologies.
Creating Your Own Galaxie Polyhedra: A Step-by-Step Guide
Galaxie polyhedra are fascinating geometric shapes that combine mathematical rigor with artistic beauty. If you're interested in exploring this unique form of art and creating your own galaxie polyhedra, this step-by-step guide will walk you through the process.
Materials Needed:
Cardstock or heavy paper
A cutting mat
A ruler
A pencil
A craft knife or scissors
Glue or double-sided tape
Step 1: Choose a Polyhedron:
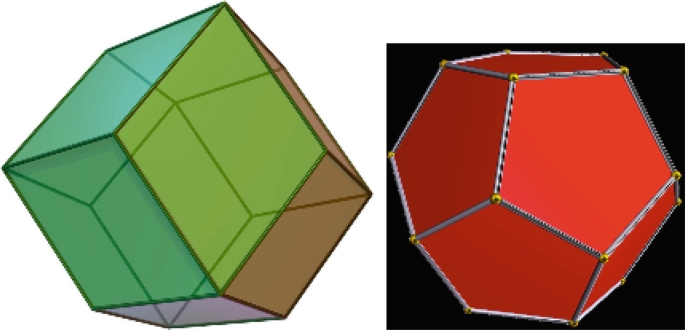
Start by selecting the type of polyhedron you want to create. There are several options to choose from, including the tetrahedron, cube, octahedron, dodecahedron, and icosahedron. Each has its own unique set of faces, edges, and vertices.
Step 2: Create a Net:
Next, you'll need to create a net for your chosen polyhedron. A net is a flattened version of the three-dimensional shape, with all the faces and tabs that will be glued together. You can find printable nets online or use a 3D modeling software to generate your own.
Step 3: Transfer the Net:
Once you have the net, transfer it onto the cardstock or heavy paper using a pencil and ruler. Make sure to label each face and tab for easier assembly later on.
Step 4: Cut Out the Shapes:
Carefully cut out each shape along the lines using a craft knife or scissors. Take your time to ensure clean and accurate cuts.
Step 5: Fold and Glue:
Now it's time to fold the tabs and start assembling the polyhedron. Follow the instructions that came with the net or use online resources to guide you through the folding and gluing process. Use glue or double-sided tape to secure the tabs in place.
Step 6: Finishing Touches:
Once the polyhedron is fully assembled, take a moment to inspect it for any loose tabs or edges. Make any necessary adjustments and reinforce them with additional glue if needed.
Congratulations! You have successfully created your own galaxie polyhedra. Display it proudly or use it as a unique decorative piece in your home.
Remember, this guide is just a starting point. Feel free to experiment with different polyhedra shapes, materials, and sizes. Let your creativity take flight as you delve into the intricate symmetry and aesthetics of galaxie polyhedra.
What are galxe polyhedra?
Galxe polyhedra are a type of mathematical shapes that exhibit complex symmetry and aesthetics. They are three-dimensional structures made up of triangles, squares, and other regular polygons, which fit together perfectly to create a harmonious and visually appealing form.
How are galxe polyhedra different from other polyhedra?
Unlike other polyhedra, galxe polyhedra have a high degree of symmetry and mathematical precision. They are characterized by their intricate geometric patterns, which form repeating motifs and symmetrical arrangements.
What is the relationship between mathematics and art in galxe polyhedra?
The relationship between mathematics and art in galxe polyhedra is intertwined. These mathematical objects not only possess aesthetic beauty but also require a deep understanding of mathematical concepts to create and appreciate them. Artists and mathematicians alike find inspiration in the symmetry, elegance, and complexity of galxe polyhedra.
How do galxe polyhedra contribute to architectural design?
Galxe polyhedra have been used in architectural design to create visually striking structures with a balance of form and function. Architects can leverage the mathematical precision and visual appeal of galxe polyhedra to design buildings that are both aesthetically pleasing and structurally sound.
Can galxe polyhedra be found in nature?
While galxe polyhedra are primarily mathematical constructions, similar geometric patterns can be found in nature. For example, the structure of certain crystals, such as quartz or diamond, often display symmetrical arrangements resembling galxe polyhedra. These natural formations are a testament to the underlying mathematical principles that govern the universe.
What are galxe polyhedra?
Galxe polyhedra are a type of 3D geometric shape that has intricate symmetry and aesthetics. They are composed of polygons and have a symmetrical arrangement of faces, edges, and vertices.
How are galxe polyhedra created?
Galxe polyhedra can be created through mathematical calculations and computer algorithms. These algorithms generate the coordinates of the vertices and connect them to form the polygons that make up the polyhedra. The resulting shapes exhibit intricate symmetry and complex geometric patterns.
Galxe login | Galxe ID | Passport | Explore Campaigns | Galxe products
2022-2024 @ From mathematics to art the intricate symmetry and aesthetics of galxe polyhedra
