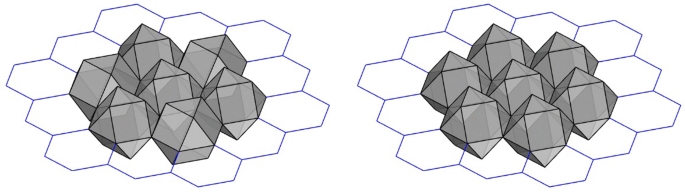
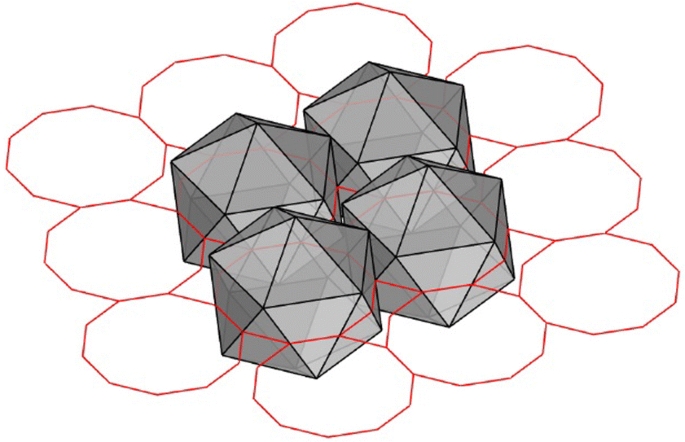
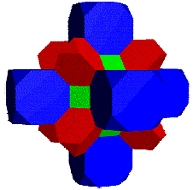
Packing and tessellation are mathematical concepts that play a crucial role in understanding the structure and arrangement of objects in space. In particular, the study of packing and tessellation of galaxy polyhedra offers fascinating insights into the intricate patterns and symmetries found in the universe.
Gone are the days when the task of arranging objects in space was thought to be solely an artistic pursuit. Today, mathematicians and scientists are uncovering the underlying principles that govern the packing and tessellation of galaxy polyhedra, shedding light on the fundamental laws that govern our cosmos.
The packaging of objects in space involves finding ways to fit them together efficiently, minimizing empty space and maximizing the use of available volume. This problem becomes particularly complex when dealing with irregular polyhedra, such as those found in galaxies. It is not just a matter of brute force packing, but rather a delicate balance between mathematical elegance and practical constraints.
The study of tessellation, on the other hand, focuses on the replication of shapes to cover a plane or fill space. A tessellation can be thought of as a tiling of the plane, where the same pattern is repeated infinitely without any gaps or overlaps. In the case of galaxy polyhedra, the intricate patterns and symmetries that emerge from tessellations reveal the underlying mathematical structures and principles that govern their formation.
Galaxy polyhedra are three-dimensional structures that can be found in the vast expanse of space. These polyhedra have complex shapes and are comprised of a multitude of interconnected faces. Understanding the mathematical principles behind the packing and tessellation of these polyhedra is of utmost importance in the field of astrophysics.
Packing refers to the arrangement of these polyhedra in space. How these polyhedra fit together and interact with each other can provide valuable insights into the formation and evolution of galaxies. By studying the packing of galaxy polyhedra, scientists can gain a better understanding of the distribution of matter in the universe, the formation of clusters and superclusters, and the behavior of dark matter.
Tessellation, on the other hand, refers to the tiling of space with these polyhedra. Just as a mosaic is created by fitting together small tiles, the tessellation of galaxy polyhedra can reveal patterns and structures on a larger scale. These tessellations can help scientists visualize and analyze complex structures in the universe, such as filaments and voids, and understand the underlying processes that shape them.
Furthermore, the study of packing and tessellation of galaxy polyhedra can also have practical applications. For instance, it can aid in the design and optimization of space telescopes and satellites, as well as the development of algorithms for detecting and analyzing galaxy clusters. It can also inspire new mathematical models and computational techniques that can be applied to other fields.
Overall, the packing and tessellation of galaxy polyhedra play a vital role in our quest to unravel the mysteries of the universe. They provide us with a unique perspective on the structure and organization of galaxies, and offer valuable insights into the fundamental processes that govern the cosmos.
Mathematical principles play a crucial role in understanding and analyzing the packing and tessellation of galxe polyhedra. These principles provide a framework for studying the geometric properties and relationships of these complex structures.
One of the key significance of mathematical principles in this context is their ability to facilitate the prediction and visualization of the packing configurations of galxe polyhedra. By applying mathematical equations and algorithms, researchers can determine the optimal ways to arrange these polyhedra in a given space.
Additionally, mathematical principles help establish the fundamental rules and constraints that govern the packing and tessellation of galxe polyhedra. These rules provide insights into the interactions and connections between the individual polyhedra, which are essential for understanding their overall stability and structural integrity.
Furthermore, mathematical principles enable the calculation of important geometric properties of galxe polyhedra, such as surface area, volume, and symmetry. These calculations help researchers quantify and compare different packing and tessellation configurations, allowing for the identification of patterns and structures that may have practical applications in various fields.
Moreover, mathematical principles contribute to the development of computational models and simulations for studying the packing and tessellation of galxe polyhedra. These models allow researchers to explore and experiment with different scenarios, providing valuable insights into the behavior and properties of these complex structures.
In conclusion, the significance of mathematical principles in the study of packing and tessellation of galxe polyhedra cannot be overstated. They provide the necessary tools and frameworks for understanding, predicting, and analyzing these intricate structures, offering valuable insights into their geometric properties and potential applications.
Mathematics plays a crucial role in understanding the complex spatial structures of various objects, including Galxe polyhedra. These mathematical principles help us analyze and make sense of the arrangements and patterns found in these structures.
One of the key concepts in understanding spatial structures is packing, which involves arranging objects in a way that maximizes their density within a given space. Mathematics provides us with algorithms and formulas that allow us to analyze and optimize the packing of objects, such as Galxe polyhedra. By utilizing mathematical models, we can determine the most efficient packing configurations and predict the behavior of these structures in different conditions.
Tessellation, another important concept, involves covering a surface with repeated geometric shapes without any gaps or overlaps. Mathematics allows us to study and analyze different types of tessellations, including those formed by Galxe polyhedra. By applying mathematical principles, we can understand the underlying properties and symmetries of these tessellations, which are essential in many fields, such as architecture, mesh generation, and crystallography.
The mathematical analysis of spatial structures also enables us to explore the relationships and interactions between different elements within these structures. By using mathematical models, we can quantify and evaluate various properties, such as connectivity, distances, and spatial arrangements. This enables us to gain a deeper understanding of the structure as a whole and how its components interact with each other.
Furthermore, mathematics provides us with tools to measure and quantify various characteristics of spatial structures. This includes parameters like volume, surface area, curvature, and angles. These measurements allow us to compare and classify different structures, evaluate their stability, and make predictions about their behavior under different conditions. Mathematics offers us a systematic and objective way to describe and analyze spatial structures, providing a common language for researchers and practitioners in various fields.
Overall, mathematics plays a fundamental role in understanding and analyzing the spatial structures found in Galxe polyhedra and other objects. It provides us with the necessary tools and techniques to explore, model, and predict the behavior of these structures. By utilizing mathematical principles, we can unlock new insights and applications in fields such as material science, architecture, and engineering.
When considering the packing and tessellation of galxe polyhedra, one important factor to consider is the relationship between packing efficiency and structural stability. Packing efficiency refers to how efficiently the polyhedra are arranged within a given space, while structural stability refers to the ability of the arrangement to maintain its shape and integrity under various external forces.
There is a direct correlation between packing efficiency and structural stability. In general, a higher packing efficiency leads to a greater structural stability, as the polyhedra are tightly packed and can support each other. When the polyhedra are loosely packed, there is more room for movement and the structure becomes less stable.
One way to understand this relationship is to consider the concept of interlocking. When the polyhedra are tightly packed and interlocked with each other, they create a strong and stable structure. The interlocking nature of the arrangement allows for the transfer of forces throughout the structure, preventing any individual polyhedra from moving or collapsing under pressure.
On the other hand, when the polyhedra are loosely packed, there is less interlocking and the structure becomes more vulnerable to external forces. The polyhedra are more likely to shift and move, potentially causing the structure to collapse. Additionally, the lack of interlocking can lead to areas of weakness within the structure, making it more susceptible to failure.
It is worth noting that while a higher packing efficiency generally leads to greater structural stability, there can be exceptions to this rule. In some cases, the specific geometry of the polyhedra or the arrangement of the packing may influence the structural stability more than the packing efficiency alone. In these cases, it is important to analyze the overall geometry and configuration of the structure to fully understand its stability.
In conclusion, the relationship between packing efficiency and structural stability is an important consideration when studying the packing and tessellation of galxe polyhedra. A higher packing efficiency generally leads to greater structural stability, as the polyhedra are tightly packed and interlocked with each other. However, other factors related to the geometry and arrangement of the packing may also impact the structural stability. Further research is needed to fully explore and understand this relationship in different contexts.
The field of materials science and engineering is heavily influenced by mathematical principles. These principles provide a framework for understanding and predicting the properties and behaviors of different materials. By applying mathematical concepts such as geometry, topology, and statistical analysis, researchers are able to design and optimize materials with specific properties for various applications.
One of the key ways that mathematical principles influence material properties is through the study of crystal structures. Crystals are highly ordered arrangements of atoms or molecules, and their properties are directly related to their underlying mathematical structure. By analyzing the symmetry and geometry of crystal structures, scientists can predict properties such as mechanical strength, electrical conductivity, and optical behavior.
Mathematical principles also play a crucial role in understanding the behavior of composites, which are materials composed of two or more distinct phases. By modeling the spatial distribution and connectivity of different components within a composite material, researchers can predict its mechanical, thermal, and electrical properties. This understanding is vital for designing composites with enhanced strength, durability, and other specific characteristics.
Tessellation, which is the process of tiling a plane with mathematical shapes, is another concept that influences material properties. By using tessellation principles, scientists can create materials with unique properties such as high porosity, stiffness, or flexibility. This can be achieved through the precise arrangement of repeating patterns or structures within a material, allowing for control over properties such as density, strength, and conductivity.
Furthermore, mathematical principles are essential in the field of nanotechnology, where materials are engineered at the atomic and molecular scale. By applying mathematical models and simulations, researchers can predict and manipulate the properties of nanomaterials, such as their electrical conductivity, mechanical strength, and catalytic activity. This understanding allows for the design and development of advanced materials with tailored properties for applications in fields such as electronics, energy storage, and biomedical engineering.
In conclusion, the influence of mathematical principles on material properties cannot be overstated. From crystal structures to composites, tessellation to nanotechnology, mathematics provides the tools and concepts necessary to understand and engineer materials with desired properties. By further advancing our understanding of these mathematical principles, researchers can continue to push the boundaries of materials science and unlock new possibilities for technological innovation.
Packing and tessellation are mathematical principles that have found immense applications in the fields of architecture and design. These concepts provide the basis for creating structures and patterns that are not only aesthetically pleasing but also efficient and functional.
One of the primary applications of packing and tessellation in architecture is the design of building facades. By utilizing these principles, architects can create intricate patterns and textures that enhance the visual appeal of a building. These patterns can be achieved by arranging different shapes or tiles in a precise manner, resulting in a cohesive and visually striking design.
In addition to enhancing the aesthetics, packing and tessellation can also play a crucial role in optimizing the use of space. By carefully arranging and packing shapes, architects can maximize the usable area within a building. This is particularly important in urban environments where space is at a premium. Efficient packing can lead to the creation of functional and flexible spaces that meet the needs of the occupants.
Tessellation, in particular, is also commonly used in the design of floor and wall coverings. By applying tessellated patterns, designers can create visually interesting surfaces that add depth and texture to a space. This can be achieved by using a variety of materials, such as tiles or stones, arranged in tessellated patterns. The result is a visually stunning design that adds character and uniqueness to the environment.
Packing and tessellation are not limited to the design of structures alone. These principles can also be applied to the design of furniture and objects. By utilizing these principles, designers can create modular and adaptable pieces that can be easily arranged and reconfigured to suit the changing needs and preferences of the user. This flexibility is particularly beneficial in spaces with limited area, where optimizing the use of space is crucial.
Furthermore, packing and tessellation can also be applied to the design of textiles and fashion. By using tessellated patterns in fabric design, designers can create visually interesting textiles that stand out and make a statement. These patterns can be achieved through the arrangement of shapes or motifs, resulting in unique and eye-catching designs.
In conclusion, the application of packing and tessellation in architecture and design is vast and diverse. From building facades to furniture design, these concepts provide designers with the tools to create visually stunning, functional, and adaptable spaces and objects. By understanding and utilizing these mathematical principles, architects and designers can push the boundaries of creativity and innovation in their respective fields.
Mathematical principles and theories are not just abstract concepts confined to the realm of academia. They have practical applications in various real-world scenarios, including packing and tessellation of geometric shapes such as galxe polyhedra. The implementation of these mathematical principles in the real world often involves the use of computer algorithms and simulations.
One practical application of mathematical principles is in the field of packaging design. When designing packaging for products, it is important to maximize the use of available space to minimize waste and transportation costs. Mathematical algorithms can be used to determine the most efficient way to pack products into containers, taking into account factors such as the shape and size of the products, as well as any constraints or limitations.
In addition to packaging design, mathematical principles are also applied in the design and construction of structures and buildings. For example, architects and engineers often use tessellation principles to create aesthetically pleasing patterns and designs in floors, walls, and ceilings. By using mathematical principles, designers can ensure that the tiles or other building materials fit together perfectly, creating a visually appealing and structurally sound result.
Packaging design
Optimal packing algorithms
Computer simulations to determine the most efficient way to pack products into containers
Architecture and construction
Tessellation principles
Using mathematical algorithms to create visually appealing and structurally sound patterns and designs
Furthermore, mathematical principles are indispensable in fields such as computer graphics and animation. Three-dimensional models and animations are based on mathematical equations and algorithms that determine the shape, movement, and behavior of objects in a virtual environment. Without the application of mathematical principles, it would be impossible to create realistic and convincing computer-generated images and animations.
In conclusion, the implementation of mathematical principles in real-world scenarios is not only possible but also highly beneficial. It allows for the optimization of various processes, ranging from packaging design to architecture and construction. By harnessing the power of mathematics, we can achieve efficient and aesthetically pleasing solutions to complex problems.
Packing and tessellation studies have been integral to various fields of science and engineering, such as materials science, crystallography, and computational geometry. However, there are still numerous areas where further advancements can be made, pushing the boundaries of our understanding and applications of packing and tessellation principles.
One potential avenue for future research lies in exploring the packing and tessellation of complex and irregular shapes. Most previous studies have focused on regular polyhedra, which have well-defined and symmetrical faces. However, real-world objects and structures often have irregular shapes that are more challenging to pack efficiently. Investigating the packing and tessellation of irregular shapes could lead to advancements in fields like transportation logistics, where optimizing the use of space is crucial for cost reduction and environmental sustainability.
Another area of potential advancement is in the development of novel packing algorithms and optimization techniques. Current algorithms, such as the well-known sphere-packing algorithm, have been successful in specific scenarios but may not be optimal for all applications. By exploring new packing algorithms and optimization techniques, researchers may be able to achieve better packing efficiency and find solutions to previously unsolved packing problems.
The incorporation of advanced computer simulation and modeling techniques is also a promising direction for future advancements in packing and tessellation studies. With the rapid advancement of computational power and algorithms, researchers can simulate and model complex packing and tessellation arrangements with greater accuracy and detail. This could lead to improved understanding of the underlying principles and enable the design of new materials with tailored properties and functionalities.
Furthermore, interdisciplinary collaborations between mathematicians, physicists, chemists, biologists, and engineers hold great potential for future advancements in packing and tessellation studies. These collaborations can foster the exchange of ideas, methodologies, and insights from different disciplines, leading to innovative approaches and breakthrough discoveries. For example, studying the packing and tessellation of biological systems, such as cells or proteins, may provide valuable insights into their functionalities and help in the development of new therapeutic interventions.
In conclusion, the field of packing and tessellation studies has significant potential for future advancements. Exploring the packing and tessellation of irregular shapes, developing novel algorithms and optimization techniques, incorporating advanced computer simulation and modeling techniques, and fostering interdisciplinary collaborations can all contribute to pushing the boundaries of our knowledge and applications of packing and tessellation principles.
The packing and tessellation of galxe polyhedra present complex mathematical and engineering challenges that require a strong collaboration between mathematicians and engineers. Both fields bring unique expertise and perspectives to the table, contributing to the development of innovative solutions.
Mathematicians play a crucial role in the initial stages of the process, using their analytical skills to understand the geometric properties and symmetries of galxe polyhedra. Through careful study and mathematical modeling, mathematicians are able to define the fundamental principles that govern the packing and tessellation of these structures.
Engineers, on the other hand, take these mathematical principles and transform them into practical solutions. They use their knowledge of materials, manufacturing processes, and structural analysis to design and construct physical prototypes. Engineers understand the constraints and challenges of real-world applications, ensuring that the mathematical models can be translated into effective and efficient designs.
The collaboration between mathematicians and engineers is a symbiotic relationship, where each field relies on the other to overcome challenges. Mathematicians provide engineers with the theoretical foundation and the mathematical tools needed to solve complex problems, while engineers offer practical insights and feedback to enhance the mathematical models.
This collaboration extends beyond the initial stages of the project. As mathematicians and engineers work together, they continually refine and improve their designs based on experimental data and feedback. This iterative process allows for the development of increasingly efficient packing and tessellation strategies, pushing the boundaries of what is possible.
In conclusion, the collaboration between mathematicians and engineers is essential in overcoming the challenges associated with the packing and tessellation of galxe polyhedra. By combining their expertise and perspectives, both fields can push the boundaries of knowledge and develop innovative solutions that have real-world applications.
What are some examples of galaxial polyhedra?
Some examples of galaxial polyhedra include the tetrahedron, octahedron, and icosahedron.
How do mathematical principles help us understand the packing and tessellation of galaxial polyhedra?
Mathematical principles help us understand the packing and tessellation of galaxial polyhedra by providing a framework for analyzing and describing their structures and relationships.
What is the significance of packing and tessellation?
Packing and tessellation plays a crucial role in various fields such as crystallography, materials science, and architecture. It allows us to understand how objects fit together and form cohesive structures.
What is the difference between packing and tessellation?
Packing refers to the arrangement of objects within a given space, while tessellation involves covering a surface with repeated geometric shapes without any gaps or overlaps.
Why are galaxial polyhedra important in mathematics?
Galaxial polyhedra are important in mathematics because they exhibit symmetrical properties and provide a foundation for studying geometric relationships and patterns.
What are galxe polyhedra?
Galxe polyhedra are three-dimensional shapes formed by connecting regular polygons. They have the property of being able to pack efficiently, meaning that they can fill space without leaving any gaps.
How are galxe polyhedra different from regular polyhedra?
Galxe polyhedra are similar to regular polyhedra, but they have some additional requirements. In addition to having regular polygons as faces, they must also satisfy certain constraints related to packing and tessellation.
What is packing in the context of galxe polyhedra?
Packing refers to the arrangement of galxe polyhedra in space without any overlap or gaps. It is a mathematical problem that seeks to find the most efficient way to fill space using these shapes.
What is tessellation?
Tessellation is the process of covering a surface with a pattern of repeated geometric shapes, such as polygons. In the context of galxe polyhedra, tessellation plays a role in determining how these shapes can be packed together to form larger structures.
What are some mathematical principles behind the packing of galxe polyhedra?
There are several mathematical principles that govern the packing of galxe polyhedra. One important principle is the concept of regularity, which means that the faces of the polyhedra must be regular polygons. Another principle is the requirement of symmetry, which helps to ensure that the polyhedra can be packed in a balanced and efficient manner.
2022-2024 @ The mathematical principles behind packing and tessellation of galxe polyhedra
To learn more about Galxe polyhedra and their mathematical properties, you can visit . This resource provides a comprehensive overview of the project, including analytics and data related to Galxe polyhedra.